
分析 (1)求出函数的导数,解关于导函数的不等式,问题转化为$a≥{({\frac{1+x}{{{x^2}+2x+2}}})_{max}}$,根据函数的单调性求出a的范围即可;
(2)取a=$\frac{1}{2}$,根据$ln({1+x})<\frac{1}{2}•\frac{{{x^2}+2x}}{1+x}$对x∈(0,+∞),均成立,令$x=\frac{k}{n^2}({k=1,2,…,n})$,作和证出结论即可.
解答 (1)解:函数h(x)的定义域为(-1,+∞),
且$h(x)=f(x)-g(x)=ln({1+x})-a•\frac{{{x^2}+2x}}{1+x}$,
则$h'(x)=\frac{1}{1+x}-a•\frac{{({2x+2})({1+x})-({{x^2}+2x})}}{{({1+{x^2}})}}=\frac{{({1+x})-a•({{x^2}+2x+2})}}{{({1+{x^2}})}}$,
由于h(x)在(-1,+∞)内单调递减,
则h'(x)≤0对x∈(-1,+∞)恒成立,
即(1+x)-a•(x2+2x+2)≤0对x∈(-1,+∞)恒成立,…(2分)
从而$a≥{({\frac{1+x}{{{x^2}+2x+2}}})_{max}}$,则$a≥{({\frac{1}{{1+x+\frac{1}{1+x}}}})_{max}}=\frac{1}{2}$,
故a的取值范围为$[{\frac{1}{2},+∞})$…(4分)
(2)证明:取$a=\frac{1}{2}$,由第(1)问可知h(x)在(0,+∞)为单调递减函数,
从而h(x)<h(0)=0;
则$ln({1+x})<\frac{1}{2}•\frac{{{x^2}+2x}}{1+x}$对x∈(0,+∞),均成立,…(6分)
令$x=\frac{k}{n^2}({k=1,2,…,n})$,
有$ln({1+\frac{k}{n^2}})<\frac{1}{2}•\frac{{{{({\frac{k}{n^2}})}^2}+2•\frac{k}{n^2}}}{{1+\frac{k}{n^2}}}=\frac{1}{2}({\frac{k}{n^2}+\frac{k}{{{n^2}+k}}})≤\frac{1}{2}({\frac{k}{n^2}+\frac{k}{{{n^2}+1}}})$;…(9分)
从而$ln[{({1+\frac{1}{n^2}})({1+\frac{2}{n^2}})…({1+\frac{n}{n^2}})}]$
=$ln({1+\frac{1}{n^2}})+ln({1+\frac{2}{n^2}})+…+ln({1+\frac{n}{n^2}})<\frac{1}{2}({\frac{1}{n^2}+\frac{2}{n^2}+…+\frac{n}{n^2}+\frac{1}{{{n^2}+1}}+\frac{2}{{{n^2}+1}}+…+\frac{n}{{{n^2}+1}}})$
=$\frac{1}{4}[{3-\frac{{n{{({n-1})}^2}+({n-1})}}{{n({{n^2}+1})}}}]≤\frac{3}{4}$,
故$({1+\frac{1}{n^2}})({1+\frac{2}{n^2}})…({1+\frac{n}{n^2}})<{e^{\frac{3}{4}}}$…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -21 | B. | -32 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 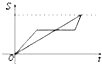 | B. | 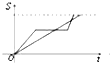 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[e-\frac{1}{e},e)$ | B. | [1,e+1) | C. | [e,e+1) | D. | $(e-\frac{1}{e},e+1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2.7岁 | B. | 3.1岁 | C. | 3.2岁 | D. | 4岁 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com