
分析 (1)14=(x2+y2+z2)(1+4+9)=(x+2y+3z)2,结合柯西不等式,即可求x+y+z的值;
(2)由不等式|x-2|<a的解集为A,求出a=1,把a=1代入函数表达式,即可求出函数f(x)=|x+a|+|x-2|的最小值.
解答 解:(1)由题14=(x2+y2+z2)(1+4+9)=(x+2y+3z)2,
但由柯西不等式,(x2+y2+z2)(1+4+9)≥(x+2y+3z)2,
当且仅当$x+2y+3z=\sqrt{14}$且$x=\frac{y}{2}=\frac{z}{3}$,即$\left\{{\begin{array}{l}{x=\frac{{\sqrt{14}}}{14}}\\{y=\frac{{2\sqrt{14}}}{14}}\\{z=\frac{{3\sqrt{14}}}{14}}\end{array}}\right.$时取等,
故取等条件必须成立,此时x+y+z=$\frac{{3\sqrt{14}}}{7}$
(2)因为$\frac{3}{2}∈A$,且$\frac{1}{2}∉A$,所以$|{\frac{3}{2}-2}|<a$,且$|{\frac{1}{2}-2}|≥a$
解得$\frac{1}{2}<a≤\frac{3}{2}$,
又因为a∈N*,所以a=1
因为|x+1|+|x-2|≥|(x+1)-(x-2)|=3
当且仅当(x+1)(x-2)≤0,即-1≤x≤2时取得等号,
所以f(x)的最小值为3
点评 本题考查柯西不等式,考查求函数的值域问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
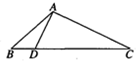 如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3,求BD的长.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3,求BD的长.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com