
���� ������������ĸ��ʣ����жϢ٣��������Ҷ��������жϢڣ����ݻ����¼��Ͷ����¼��Ķ��壬���жϢۣ����ݳ�Ҫ�����Ķ��壬���жϢܣ��ж�ԭ���������������٣����жϢݣ�
��� �⣺����ʵ��x��y��[-1��1]��������x2+y2��1�ĸ���Ϊ1-$\frac{��}{4}$���ʴ���
���ڡ�ABC�У���A��B��?��a��b��?��2RsinA��2RsinB��?��sinA��sinB����
�ʡ�A��B���ǡ�sinA��sinB���ij�Ҫ����������ȷ��
�ۡ�A1��A2�ǻ����¼���ʱ����A1��A2��һ���Ƕ����¼�����
��A1��A2�Ƕ����¼���ʱ����A1��A2�ǻ����¼���
�����⡰A1��A2�ǻ����¼��������⡰A1��A2�Ƕ����¼����ı�Ҫ���������������ȷ��
����a��b��ʵ����
��a��1��b��1��ʱ����a+b��2��ab��1��������
��a��1��b��1��ʱ����a+b��2��ab��1����һ��������
��a��1��b��1���ǡ�a+b��2��ab��1���ij�ֲ���Ҫ����������ȷ��
����x��1��y��1ʱ��x+y��2��Ϊ�����⣬
����������⣺��x+y��2����x��1��y��1Ϊ�����⣮����ȷ��
�ʴ�Ϊ���ڢۢܢ�
���� ���������������ж���Ӧ��Ϊ���壬�����˼��θ��ͣ���Ҫ�������������⣬�Ѷ��е���


 ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��Բ�ĵ���뾶r=1��ĸ�߳�Ϊ4��
��ͼ��Բ�ĵ���뾶r=1��ĸ�߳�Ϊ4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
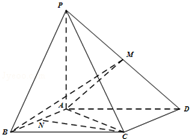 ��ͼ������P-ABCD�У�����ABCDΪƽ���ı��Σ�PA�͵���ABCD��M����PD���е㣬��PA=AB=AC=2��BC=2$\sqrt{2}$��
��ͼ������P-ABCD�У�����ABCDΪƽ���ı��Σ�PA�͵���ABCD��M����PD���е㣬��PA=AB=AC=2��BC=2$\sqrt{2}$�� �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ֱ��lƽ����ƽ����ڵ�������ֱ�ߣ���l�Φ� | |
| B�� | ��ֱ��a?������a�Φ� | |
| C�� | ��ֱ��a�Φ���b?������a��b | |
| D�� | ��ֱ��a��b��b?����ֱ��aƽ����ƽ���ڵ�������ֱ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | �Ȳ�����ֲ���Ҫ���� | ||
| C�� | ��Ҫ���� | D�� | ��Ҫ��������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com