
分析 (1)求出a=2时,h(x)的导数,令导数大于0,得增区间;令导数小于0,得减区间;
(2)分别求出f(x)的最小值,令h(x)=f′(x)-g′(x)=$\frac{lnx-1}{(lnx)^{2}}$-a,求出h(x),判断单调性即可得到h(x)的最大值,再由题意可得f(x)的最小值不大于h(x)的最大值,解不等式即可得到a的范围.
解答 解:(1)若a=2,则h(x)=f(x)+g(x)=$\frac{x}{lnx}$+2x+1,
h′(x)=$\frac{lnx-1}{(lnx)^{2}}$+2=$\frac{(2lnx-1)(lnx+1)}{(lnx)^{2}}$,
当x>$\sqrt{e}$时,h′(x)>0,h(x)在($\sqrt{e}$,+∞)递增;
当1<x<$\sqrt{e}$时,h′(x)<0,h(x)在(1,$\sqrt{e}$)递减.
则有h(x)的单调增区间为($\sqrt{e}$,+∞),单调减区间为(1,$\sqrt{e}$);
(2)f′(x)=$\frac{lnx-1}{(lnx)^{2}}$,g′(x)=a,
当1<x<e时,f′(x)<0,f(x)在(1,e)递减;
当e<x≤e2时,f′(x)>0,f(x)在(e,e2]递增.
则有x=e,f(x)取得最小值,且为$\frac{e}{lne}$=e.
令h(x)=f′(x)-g′(x)=$\frac{lnx-1}{(lnx)^{2}}$-a,
h′(x)=$\frac{1}{x}$•$\frac{2-lnx}{(lnx)^{3}}$,当1<x≤e2时,h′(x)>0,h(x)在(1,e2]递增,
则有x=e2,h(x)取得最大值,且为$\frac{1}{4}$-a,
由?x1、x2∈(1,e2],f(x1)≤f′(x2)-g′(x2)成立,
可得e≤$\frac{1}{4}$-a,
解得a≤$\frac{1}{4}$-e.
故实数a的取值范围为(-∞,$\frac{1}{4}$-e].
点评 本题考查导数的运用:求单调区间和极值、最值,同时考查不等式成立问题转化为求函数的最值问题,考查运算化简能力,属于中档题和易错题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
 如图是一个长方体ABCD-A1B1C1D1被一个平面截去一部分后,所得多面体的直观图,已知AB=6,AD=AA1=4,BE=CF=2.
如图是一个长方体ABCD-A1B1C1D1被一个平面截去一部分后,所得多面体的直观图,已知AB=6,AD=AA1=4,BE=CF=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
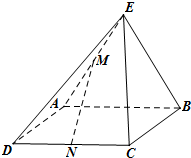 如图,矩形ABCD所在平面与直角三角形ABE所在平面互相垂直,AE⊥BE,点M,N分别是AE,CD的中点.
如图,矩形ABCD所在平面与直角三角形ABE所在平面互相垂直,AE⊥BE,点M,N分别是AE,CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com