
分析 (Ⅰ)由椭圆离心率为$\frac{1}{2}$,直线$y=x+\sqrt{6}$与以原点为圆心,以椭圆E的短半轴长为半径的圆相切,列出方程求出a,b,由此能求出椭圆E的方程.
(Ⅱ)令l:y=kx+m(k≠0),联立$\left\{{\begin{array}{l}{y=kx+m}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$,得(3+4k2)x2+8kmx+4(m2-3)=0,由此利用韦达定理、根的判别式,向量数量积、圆的性质,结合已知条件能证明直线l过定点,并求出该定点的坐标.
解答 解:(Ⅰ)∵$e=\frac{1}{2}$,∴$\frac{c}{a}=\frac{1}{2}$.
∵直线$y=x+\sqrt{6}$与以原点为圆心,以椭圆E的短半轴长为半径的圆相切,
∴$r=\frac{{|{\sqrt{6}}|}}{{\sqrt{1+1}}}=b$,解得$b=\sqrt{3}$,a=2.
∴椭圆E的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
证明:(Ⅱ)令l:y=kx+m(k≠0)
设A(x1,y1),B(x2,y2),取立$\left\{{\begin{array}{l}{y=kx+m}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$,
联立消y得(3+4k2)x2+8kmx+4(m2-3)=0
∴$\left\{{\begin{array}{l}{{x_1}+{x_2}=-\frac{8km}{{3+4{k^2}}}}\\{{x_1}{x_2}=\frac{{4({m^2}-3)}}{{3+4{k^2}}}}\end{array}}\right.$,…(6分)
且△=64k2m2-16(3+4k2)(m2-3)>0,
整理得:4k2>m2-3,
∵以AB为直径的圆过右顶点N(2,0)
∴$\overrightarrow{NA}•\overrightarrow{NB}=({x_1}-2)({x_2}-2)+{y_1}{y_2}=7{m^2}+4{k^2}+16km=0$,
化简得$7{(\frac{m}{k})^2}+16\frac{m}{k}+4=0$,
∴$\frac{m}{k}=-\frac{2}{7}$,或$\frac{m}{k}=-2$,…(10分)
∵当$\frac{m}{k}=-2$时.l:y=k(x-2)过定点N(2,0)不合题意
∴$\frac{m}{k}=-\frac{2}{7}$,故$l:y=k(x-\frac{2}{7})$过定点$N(\frac{2}{7},0)$.…(12分)
点评 本题考查椭圆方程的求法,考查直线过定点的证明,考查圆、椭圆、韦达定理、根的判别式,向量数量积等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
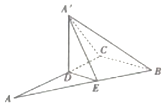 如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.
如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,-2) | C. | (-∞.-1)∪(1,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
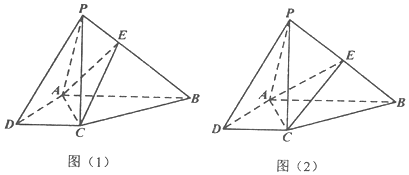
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com