
���� ������{an}�Ĺ���Ϊd�����õȲ����е�ͨ�ʽ�����ʽ����ϵȱ����е���������ʣ��ⷽ�̿ɵ������������õ�����
�������$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{��2n-1����2n+1��}$=$\frac{1}{2}$��$\frac{1}{2n-1}$-$\frac{1}{2n+1}$������������������Ϳɵ�Tn�����ò�����������еĵ����ԣ��ɵ���Сֵ�����ɵõ�������k����Сֵ��
��� �⣺������{an}�Ĺ���Ϊd��
��a3=5����a1��a2��a5�ɵȱ����У�
�ɵ�a22=a1a5��
��$\left\{\begin{array}{l}{a_1}+2d=5\\{��{a_1}+d��^2}={a_1}��{a_1}+4d��\end{array}\right.$��
��$\left\{\begin{array}{l}{a_1}=1\\ d=2\end{array}\right.$��
��an=2n-1��Sn=$\frac{1}{2}$��1+2n-1��n��
�ɵ�${S_n}={n^2}$��
����$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{��2n-1����2n+1��}$=$\frac{1}{2}$��$\frac{1}{2n-1}$-$\frac{1}{2n+1}$����
${T_n}=\frac{1}{2}��1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+��+\frac{1}{2n-1}-\frac{1}{2n+1}��=\frac{n}{2n+1}$��
��$\frac{n}{2n+1}��\frac{9}{{{{��n+k��}^2}}}$��
��${��n+k��^2}��9��2+\frac{1}{n}��$�������
��$k��3\sqrt{2+\frac{1}{n}}-n$��
$��{c_n}=3\sqrt{2+\frac{1}{n}}-n$����{cn}�ǵݼ����У�
��$k��{c_1}=3\sqrt{3}-1$��
��kmin=5��
���� ���⿼��Ȳ����е�ͨ�ʽ�����ʽ�����ã�����ȱ����е���������ʣ��Լ����е���ͷ���������������ͣ�ͬʱ���鲻��ʽ���������Ľⷨ��ע�����÷�����������еĵ����ԣ������ֵ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{7}$ | B�� | $\frac{3}{7}$ | C�� | $\frac{4}{7}$ | D�� | $\frac{5}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
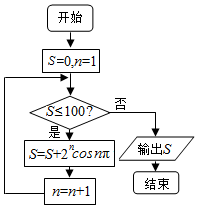
| A�� | $\frac{{{2^{99}}-2}}{3}$ | B�� | $\frac{{{2^{100}}-2}}{3}$ | C�� | $\frac{{{2^{101}}-2}}{3}$ | D�� | $\frac{{{2^{102}}-2}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{3}}}{4}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{3}{2}+\frac{3}{2}i$ | B�� | $-\frac{3}{2}-\frac{3}{2}i$ | C�� | $-\frac{3}{2}+3i$ | D�� | $-\frac{3}{2}-3i$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com