
���� ���ݿռ�ֱ�ߺ�ƽ��ƽ�л�ֱ�����ʷֱ�����жϼ��ɣ�
��� �⣺�ٸ�������ƽ�е����ʣ�ͬʱ��һ��ƽ��ƽ�е�����ƽ����ƽ�еģ���$\left.\begin{array}{l}���Φ�\\ ���Φ�\end{array}\right\}⇒�¡Φ�$��ȷ��
�ڵ�m�Φ�ʱ��m��¿����ཻ������ƽ�У�Ҳ������ƽ���ڣ���$\left.\begin{array}{l}���ͦ�\\ m�Φ�\end{array}\right\}⇒m�ͦ�$����
�۸������洹ֱ������ƽ�е����ʿɵ�$\left.\begin{array}{l}m�ͦ�\\ m�Φ�\end{array}\right\}⇒���ͦ�$��ȷ��
��$\left.\begin{array}{l}m��n\\ n?��\end{array}\right\}⇒m�Φ�$�����п�����m?ƽ������ʢܴ���
����ȷ���Ǣ٢ۣ�
�ʴ�Ϊ���٢ۣ�
���� ������Ҫ�������������жϣ��漰�ռ�ֱ�ߣ�ƽ��֮��ƽ�л�ֱ���жϣ�������Ӧ���ж������Լ����ʶ����ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9x+y-5=0 | B�� | 9x-y-4=0 | C�� | 2x+y-2=0 | D�� | x+y-5=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
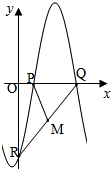 ��ͼ������$f��x��=Asin{����x+�գ�_{\;}}��A��0���أ�0��|��|��\frac{��}{2}��$�����������������P��Q��R����P��2��0������PQR=$\frac{��}{4}$��MΪQR���е㣬PM=2$\sqrt{5}$����A��ֵΪ-$\frac{16\sqrt{3}}{3}$��
��ͼ������$f��x��=Asin{����x+�գ�_{\;}}��A��0���أ�0��|��|��\frac{��}{2}��$�����������������P��Q��R����P��2��0������PQR=$\frac{��}{4}$��MΪQR���е㣬PM=2$\sqrt{5}$����A��ֵΪ-$\frac{16\sqrt{3}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{3\sqrt{3}}}{4}$ | B�� | $\frac{{\sqrt{3}}}{4}$ | C�� | $\frac{{3\sqrt{3}}}{2}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | 3 | D�� | -3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com