练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知f（x）是奇函数，当x＜0时，f（x）=x3+x2，则f（2）=
     
    ．
    考点：函数奇偶性的性质
    专题：函数的性质及应用
    分析：本题利用函数f（x）是奇函数，将f（2）转化为求f（-2），再用当x＜0时，f（x）=x3+x2，求出f（-2）的值，从而得到本题结论．
    解答： 解：∵函数f（x）是奇函数，
    ∴f（-x）=f（x）．
    ∴f（2）=-f（-2）．
    ∵当x＜0时，f（x）=x3+x2，
    ∴f（-2）=（-2）3+（-2）2=-4．
    ∴f（2）=4．
    故答案为4．
    点评：本题考查了用函数的奇偶性求函数的值，本题难度不大，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知集合D={x|
    24-x
    x-9
    ＞0    }，若a，b∈D且
    1
    a
    +
    1
    2b
    =
    1
    12
    ，则9a•3b的最小值为（　　）
    A、27
    B、327
    C、54
    D、354

    查看答案和解析>>

    科目：高中数学 来源： 题型：

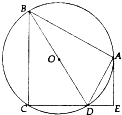    如图，⊙O是四边形ABCD的外接圆，BD是⊙O的直径，AE⊥CD于点E，∠BDA=∠EDA．
    （1）证明：AE2=CE•DE；
    （2）如果AB=6，AE=3，求BC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设复数z=（a2+a-2）+（a2-7a+6）i，其中a∈R，当a取何值时，
    （1）z∈R；  
    （2）z是纯虚数；   
    （3）
    .
    z
    =28+4i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求曲线y=sinx，y=cosx与直线x=0，x=
    π
    2
    所围成的平面图形（阴影部分）的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知在△ABC中，已知a=
    		3
    ，b=3，∠C=30°，则∠A=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

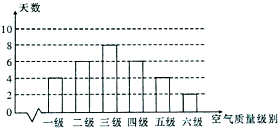    根据空气质量指数AQJ（为整数）的不同，可将空气质量分级如下表：
    某市2014年11月1日-11月30日，对空气质量指数AQI进行监测，获得数据后得到如条形图：
    （1）市教育局规定在空气质量类别达到中度污染及以上时学生不宜进行户外跑步活动，估计该城市本月（按30天计）学生可以进行户外跑步活动的概率；
    （2）在上述30个监测数据中任取2个，设ξ为空气质量类别颜色为绿色的天数，求ξ的分布列与数学期望．
    AQI（数值）0～5051～100101～150151～200201～300＞300
    空气质量级别一级二级三级四级五级六级
    空气质量类别优良轻度污染中度污染重度污染严重污染
    空气质量类别颜色绿色黄色橙色红色紫色褐红色

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    过点P（1，2）的直线，将圆形区域{（x，y）|x2+y2≤9}分为两部分，使这两部分的面积之差最大，则该直线的方程为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    执行如图所示的程序框图，则输出结果S的值为（　　）
    A、
    1
    2
    B、0
    C、-
    3
    2
    D、-1

    查看答案和解析>>

    同步练习册答案