
| A. | 0 | B. | ±$\sqrt{3}$ | C. | 0或$\sqrt{3}$ | D. | 0或±$\sqrt{3}$ |
分析 已知等式左边利用二倍角的余弦函数公式化简,整理求cosθ的值,利用同角三角函数间基本关系求出sinθ的值,原式第一项利用二倍角的正弦函数公式化简后,将各自的值代入计算即可求出值.
解答 解:由cos2θ+cosθ=0,得2cos2θ+cosθ-1=0,即(cosθ+1)(2cosθ-1)=0,
解得:cosθ=-1或cosθ=$\frac{1}{2}$,
当cosθ=-1时,sinθ=0,此时sin2θ+sinθ=2sinθcosθ+sinθ=0;
当cosθ=$\frac{1}{2}$时,sinθ=$\frac{\sqrt{3}}{2}$或-$\frac{\sqrt{3}}{2}$,此时sin2θ+sinθ=2sinθcosθ+sinθ=$\sqrt{3}$或-$\sqrt{3}$,
综上,sin2θ+sinθ=0或$\sqrt{3}$或-$\sqrt{3}$.
故选:D.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键,属于基础题.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
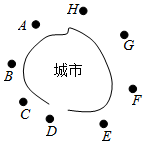 某海滨城市外围有8个小岛,如图,某中学决定分两次去这8个小岛进行社会调查,每次去4个,要求每次至多只能连续两个小岛相邻(如允许ABDE,但不允许ABCE),则能够有30种安排方法.
某海滨城市外围有8个小岛,如图,某中学决定分两次去这8个小岛进行社会调查,每次去4个,要求每次至多只能连续两个小岛相邻(如允许ABDE,但不允许ABCE),则能够有30种安排方法.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示是一打靶用的靶标,其半径为10cm,被平分成10个同心圆,从里到外各区域分别记在数值10,9,…,2,1,表示打到那个区域就得对应的分值,若某运动员打靶所得分值ξ与打中相应区域的概率P(ξ)的函数关系是P(ξ)=$\frac{1}{55}$(11-ξ).
如图所示是一打靶用的靶标,其半径为10cm,被平分成10个同心圆,从里到外各区域分别记在数值10,9,…,2,1,表示打到那个区域就得对应的分值,若某运动员打靶所得分值ξ与打中相应区域的概率P(ξ)的函数关系是P(ξ)=$\frac{1}{55}$(11-ξ).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 任意三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com