
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 1 |
分析 曲线是以C(4,6)为圆心,以$\sqrt{2}$为半径的圆,$\frac{y}{x}$是原点和圆上的点的连线的斜率,当原点和圆上的点的连线是切线OA时,$\frac{y}{x}$取最值,由此能求出$\frac{y}{x}$的最小值.
解答 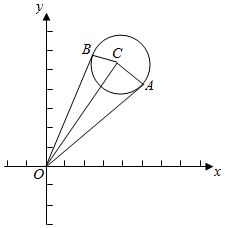 解:曲线方程$\left\{\begin{array}{l}x=4+\sqrt{2}cosθ\\ y=6+\sqrt{2}sinθ\end{array}\right.$(θ为参数)化为普通方程得(x-4)2+(y-6)2=2,
解:曲线方程$\left\{\begin{array}{l}x=4+\sqrt{2}cosθ\\ y=6+\sqrt{2}sinθ\end{array}\right.$(θ为参数)化为普通方程得(x-4)2+(y-6)2=2,
∴曲线是以C(4,6)为圆心,以$\sqrt{2}$为半径的圆,
∴$\frac{y}{x}$是原点和圆上的点的连线的斜率,
如图,当原点和圆上的点的连线是切线OA时,$\frac{y}{x}$取最小值,
设过原点的切线方程为y=kx,
则圆心C(4,6)到切线y=kx的距离:
d=$\frac{|4k-6|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$,即7k2-24k+17=0,
解得k=1或k=$\frac{17}{7}$,
∴$\frac{y}{x}$的最小值是1.
故选:D.
点评 本题考查圆上的点的纵坐标与横坐标的比值的最小值的求法,考查参数方程、直角坐标方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 200,20 | B. | 400,40 | C. | 200,40 | D. | 400,20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\sqrt{2}+1$ | D. | $\frac{{\sqrt{2}+1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C(2,1),r=5 | B. | C(2,-1),r=$\sqrt{5}$ | C. | C(2,-1),r=5 | D. | C(-2,1),r=$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\hat y=-0.3x+4.4$ | B. | $\hat y=-2x+9.5$ | C. | $\hat y=2x-2.4$ | D. | $\hat y=0.4x+2.3$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com