
【题目】第十二届全国人名代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(1)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
(2)根据题意建立![]() 列联表,并判断是否有99%的把握认为男生与女生对两会的关注有差异?
列联表,并判断是否有99%的把握认为男生与女生对两会的关注有差异?
附:  ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【答案】(1)没有99%的把握认为男生与女生对两会的关注有差异;(2)![]() .
.
【解析】【试题分析】(1)可先设男生比较关注和不太关注的人分别为![]() ,则女生比较关注和不太关注的为
,则女生比较关注和不太关注的为![]() ,建立方程组
,建立方程组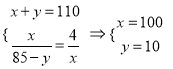 ,由此可得
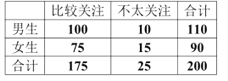
,由此可得![]() 列联表为:
列联表为:
 ,然后运用计算公式算出
,然后运用计算公式算出![]() ,借助表中的参数可以断定没有99%的把握认为男生与女生对两会的关注有差异;(2)先由分层抽样的知识点算得:在男生和女生中分别抽取的人数为4人、3人,再运用古典概型的计算公式算得其概率
,借助表中的参数可以断定没有99%的把握认为男生与女生对两会的关注有差异;(2)先由分层抽样的知识点算得:在男生和女生中分别抽取的人数为4人、3人,再运用古典概型的计算公式算得其概率![]() .
.
解: (1)设男生比较关注和不太关注的人分别为![]() ,则女生比较关注和不太关注的为
,则女生比较关注和不太关注的为![]() ,
,
则由题意得: 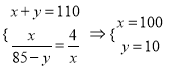 ,因此可得
,因此可得![]() 列联表为:
列联表为:

∴![]() ,所以没有99%的把握认为男生与女生对两会的关注有差异.
,所以没有99%的把握认为男生与女生对两会的关注有差异.
(2)由分层抽样的知识点可得:在男生和女生中分别抽取的人数为4人、3人.
则![]() .
.


科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄”45岁为分界点,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在![]() 和
和![]() 的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在
的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在![]() 的概率.
的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: 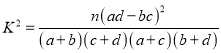 (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下列材料,回答后面问题:
在2014年12月30日![]() 播出的“新闻直播间”节目中,主持人说:“……加入此次亚航失联航班
播出的“新闻直播间”节目中,主持人说:“……加入此次亚航失联航班![]() 被证实失事的话,2014年航空事故死亡人数将达到1320人.尽管如此,航空安全专家还是提醒:飞机仍是相对安全的交通工具.①世界卫生组织去年公布的数据显示,每年大约有124万人死于车祸,而即使在航空事故死亡人数最多的一年,也就是1972年,其死亡数字也仅为3346人;②截至2014年9月,每百万架次中有2.1次(指飞机失事),乘坐汽车的百万人中其死亡人数在100人左右.”
被证实失事的话,2014年航空事故死亡人数将达到1320人.尽管如此,航空安全专家还是提醒:飞机仍是相对安全的交通工具.①世界卫生组织去年公布的数据显示,每年大约有124万人死于车祸,而即使在航空事故死亡人数最多的一年,也就是1972年,其死亡数字也仅为3346人;②截至2014年9月,每百万架次中有2.1次(指飞机失事),乘坐汽车的百万人中其死亡人数在100人左右.”
对上述航空专家给出的①、②两段表述(划线部分),你认为不能够支持“飞机仍是相对安全的交通工具”的所有表述序号为__________,你的理由是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题,其中正确的个数有( )
①由独立性检验可知,有![]() 的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在线性回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
④对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
, ![]() 为原点,
为原点, ![]() ,
, ![]() 是
是![]() 轴上的两个动点,且
轴上的两个动点,且![]() ,直线
,直线![]() 和
和![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
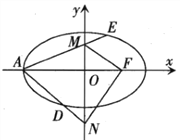
(Ⅰ)求![]() 的面积的最小值;
的面积的最小值;
(Ⅱ)证明: ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2 ![]() . (Ⅰ)判断f(x)奇偶性并证明;
. (Ⅰ)判断f(x)奇偶性并证明;
(Ⅱ)用单调性定义证明函数g(x)= ![]() 在函数f(x)定义域内单调递增,并判断f(x)=log2
在函数f(x)定义域内单调递增,并判断f(x)=log2 ![]() 在定义域内的单调性.
在定义域内的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)=(x﹣l)(log3a)2﹣6(log3a)x+x+l在x∈[0,l]内恒为正值,则a的取值范围是( )
A.﹣1<a< ![]()
B.a< ![]()
C.a> ![]()
D.![]() <a<
<a< ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]()
(1)求函数f(x)的解析式;
(2)若方程3[f(x)]2﹣f(x)+m=0在x∈( ![]() ,
, ![]() )内有两个不同的解,求实数m的取值范围.
)内有两个不同的解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com