
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=| 1 |
| 2 |
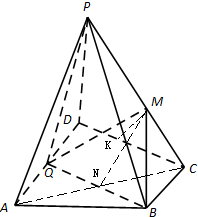 解:(1)证明:连接AC交BQ于N,连接MN,
解:(1)证明:连接AC交BQ于N,连接MN,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| m |
| n |
| 12 |
| 5 |
| m |
| n |
| π |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某种商品在50个不同地区的零售价格全部介于13元与18元之间,将各地价格按如下方式分成五组:第一组[13,14);第二组[14,15),…,第五组[17,18].如图是按上述分组方法得到的频率分布直方图.
某种商品在50个不同地区的零售价格全部介于13元与18元之间,将各地价格按如下方式分成五组:第一组[13,14);第二组[14,15),…,第五组[17,18].如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,点A,B,C均在单位圆上,已知点A在第一象限用横坐标是
如图,在平面直角坐标系xOy中,点A,B,C均在单位圆上,已知点A在第一象限用横坐标是| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com