Question

15．有大小形状完全相同的4个红球，2个白球，放入如图所示的九个格子中，每个格子至多放入1个小球，相邻格子（即有公共边的两个正方形）中放入的小球不同色，则不同的方法共有（　　）

• A． 32种
• B． 40种
• C． 48种
• D． 56种

Answer 1

分析 对红球的位置分类讨论：第一类，当4个红球在4个顶角的位置时，白球放在除最中间后剩下4个格种任选两个；第二类，当有一个红球再最中间时，其它三个红球只能放在顶角位置，当其中一个白球在顶角时，另一个白球只有2种方法，当白球不在顶角时，白球放在除顶角后剩下4个格种任选两个；第三类，当4个红球放在每外围三个格的中间时，白球从红球放在剩下5个格种任选两个，即可得出．

解答 解：第一类，当4个红球在4个顶角的位置时，白球放在除最中间后剩下4个格种任选两个，故有${∁}_{4}^{2}$=6种，如图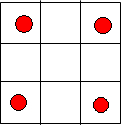

第二类，当有一个红球再最中间时，其它三个红球只能放在顶角位置，有${∁}_{4}^{3}$=4种，
当其中一个白球在顶角时，另一个白球只有2种方法，当白球不在顶角时，白球放在除顶角后剩下4个格种任选两个有${∁}_{4}^{2}$=6种，故有4×（2+6）=32种，如图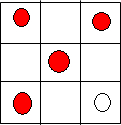

第三类，当4个红球放在每外围三个格的中间时，白球从红球放在剩下5个格种任选两个有${∁}_{5}^{2}$=10种，如图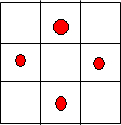

根据分类计数原理，故有6+32+10=48．
故选：C．

点评 本题考查了排列组合数的应用、分类讨论思想方法，考查了推理能力与计算能力，属于中档题．