练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     甲、乙两支足球队鏖战90分钟踢成平局，加时赛30分钟后仍成平局，现决定各派5名队员，每人射一点球决定胜负，设甲、乙两队每个队员的点球命中率均为0.5.

    (1) 不考虑乙队，求甲队仅有3名队员点球命中，且其中恰有2名队员连续命中的概率；

    (2) 求甲、乙两队各射完5个点球后，再次出现平局的概率．

    解：(1) 甲队3名队员射中，恰有2名队员连续命中的情形有A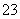种，故所求的概率为


    P1＝A×0.53×(1－0.5)2＝.

    (2) 再次出现平局包括0∶0，1∶1，…，5∶5等6种可能性，故其概率为

    P2＝[C×0.50×(1－0.5)5]2＋[C×0.51×(1－0.5)4]2＋…＋[C×0.55×(1－0.5)0]2＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如下图，共有多少个不同的三角形？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在0，1，2，3，…，9这十个自然数中，任取三个不同的数字．将取出的三个数字按从小到大的顺序排列，设ξ为三个数字中相邻自然数的组数(例如：若取出的三个数字为0，1，2，则相邻的组为0，1和1，2，此时ξ的值是2)，求随机变量ξ的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在4次独立试验中，事件A出现的概率相同，若事件A至少发生1次的概率是，则事件A在一次试验中出现的概率是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为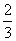，中奖可以获得2分；方案乙的中奖率为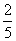，中奖可以得3分；未中奖则不得分．每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品．

    若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为X，求X≤3的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某人进行射击，每次中靶的概率均为0.8，现规定：若中靶就停止射击，若没中靶，则继续射击，如果只有3发子弹，则射击数X的均值为________．(填数字)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    　某电器商经过多年的经验发现本店每个月售出的电冰箱的台数ξ是一个随机变量，它的分布列为P(ξ＝i)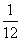＝(i＝1，2，…，12)；设每售出一台电冰箱，电器商获利300元．如销售不出，则每台每月需花保管费100元. 问电器商每月初购进多少台电冰箱才能使月平均收益最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，E、F分别为AC、AB的中点，BE与CF相交于G点，设＝a，＝b，试用a，b表示.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    齐王与田忌赛马，田忌的上马优于齐王的中马，劣于齐王的上马，田忌的中马优于齐王的下马，劣于齐王的中马，田忌的下马劣于齐王的下马，现各出上、中、下三匹马分组进行比赛．

    (1) 如果双方均不知道对方马的出场顺序，求田忌获胜的概率；

    (2) 为了得到更大的获胜概率，田忌预先了解到齐王第一场必出上等马．那么，田忌怎样安排出马顺序，才能使自己获胜的概率最大？

    查看答案和解析>>

    同步练习册答案