练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知平面a及空间中的任意一条直线l那么在平面a内一定存在直线b使得（　　）
    A．l∥bB．l与b相交C．l与b是异面直线D．l⊥b

    分析 本题可以从直线与平面的位置关系入手：直线与平面的位置关系可以分为三种：直线在平面内、直线与平面相交、直线与平面平行，在这三种情况下在讨论平面中的直线与已知直线的关系，通过比较可知：每种情况都有可能垂直．

    解答 解：当直线a与平面α相交时，
    平面α内的任意一条直线与直线a的关系只有两种：异面、相交，此时就不可能平行了，故A错．
    当直线a与平面α平行时，
    平面α内的任意一条直线与直线a的关系只有两种：异面、平行，此时就不可能相交了，故B错．
    当直线a在平面α内时，
    平面α内的任意一条直线与直线a的关系只有两种：平行、相交，此时就不可能异面了，故C错．
    不管直线a与平面α的位置关系相交、平行，还是在平面内，
    都可以在平面α内找到一条直线与直线b垂直，
    因为直线在异面与相交时都包括垂直的情况，故D正确．
    故选D．

    点评 本题主要考查了空间中直线与直线之间的位置关系，空间中直线与平面之间的位置关系，考查空间想象能力和思维能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知复数z：满足（1+$\sqrt{3}$i）z=1+i，则|z|等于（　　）
    A．$\frac{\sqrt{2}}{2}$B．-$\sqrt{2}$C．$\sqrt{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

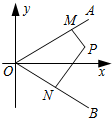    5．如图，射线OA，OB所在的直线的方向向量分别为$\overrightarrow{d_1}=（{1，k}）$，$\overrightarrow{d_2}=（{1，-k}）（{k＞0}）$，点P在∠AOB内，PM⊥OA于M，PN⊥OB于N；
    （1）若k=1，$P（{\frac{3}{2}，\frac{1}{2}}）$，求|OM|的值；
    （2）若P（2，1），△OMP的面积为$\frac{6}{5}$，求k的值；
    （3）已知k为常数，M，N的中点为T，且${S_{△MON}}=\frac{1}{k}$，当P变化时，求|OT|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知等比数列{bn}前n项和为Sn=3n-k，公差为k的等差数列{an}满足：b1=a1，求{an}，{bn}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=ax2-（a+2）x+lnx．
    （Ⅰ）当a=0时，求函数y=f（x）在点（1，f（1））处的切线方程；
    （Ⅱ）若f（x）在区间（1，e）的有零点，求正数a的取值范围；
    （Ⅲ）求证不等式${e^{\sum_{i=1}^n{\frac{i+1}{i^2}}}}＞n$对任意的正整数n都成立（其中e是自然对数的底数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．如图所示，曲线C由上半圆C1：x2+y2=1（y≥0）和部分抛物线C2：y=x2-1（y≥0）连接而成，A，B为C1与C2的公共点（B在原点右侧），过C1上的点D（异于点A，B）的切线l与C2分别相交于M，N两点．
    （1）若切线l与抛物绩y=x2-1在点D处的切线平行，求点D的坐标．
    （2）若点D（x0，y0）勾动点时，求证∠MON恒为钝角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若复数z满足（2+i）z=1+2i（i是虚数单位），则z的共轭复数所对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知在直角梯形ABCD中，AB∥CD，AB⊥AD，AB=AD=2，CD=1，P为线段BC上一个动点，设$\overrightarrow{BP}=λ\overrightarrow{BC}$，则当$\overrightarrow{PA}•\overrightarrow{PD}$取得最小值时λ的值是（　　）
    A．$\frac{1}{2}$B．$\frac{4}{5}$C．0D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．不等式x2（x-1）（x+4）≥0的解集为{x|x≥1或x≤-4或x=0}．

    查看答案和解析>>

    同步练习册答案