
 对某个品牌的U盘进行寿命追踪调查,所得情况如下面频率分布直方图所示.
对某个品牌的U盘进行寿命追踪调查,所得情况如下面频率分布直方图所示.分析 (1)图根据频率分布直方图进行求解;
(2)利用分层抽样的定义建立比例关系即可得到结论.
(3)利用列举法进行求解.
解答 解:(1)∵0.01×10+20y0+0.02×10+0.04×10=1,∴y0=0.015(2分)
(2)10~30万次之间的U盘所占频率为0.01×10+0.015×10=0.25,
设10~30万次之间的U盘应抽取x个,$\frac{x}{20}=0.25$,∴x=5 (4分)
(3)10~20万次应抽取20×10×0.01=2个,设为a1,a2,
20~30万次应抽取20×10×0.015=3个,
设为b1,b2,b3,寿命落在1030万次之间的元件中任取2个元件,一切可能结果组成的基本事件空间为$Ω=\left\{\begin{array}{l}({a_1},{a_2}),({a_1},{a_3}),({a_1},{b_1}),({a_1},{b_2}),({a_2},{a_3})\\({a_2},{b_1}),({a_2},{b_2}),({a_3},{b_1}),({a_3},{b_2}),({b_1},{b_2})\end{array}\right\}$
“抽取的两个U盘恰好有一个寿命为1020万次,一个寿命为2030万次”为事件A,则A={(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2)},
则对应的概率$P(A)=\frac{6}{10}=\frac{3}{5}$.(8分)
点评 本题主要考查概率和统计和分层抽样的应用,根据条件建立比例关系以及利用列举法求概率是解决本题的关键.比较基础.


科目:高中数学 来源: 题型:选择题
| A. | 正数m的平方不等于0 | B. | 若m不是正数,则它的平方等于0 | ||
| C. | 若m不是正数,则它的平方不等于0 | D. | 非正数m的平方等于0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称为左视图),其中正视图和侧视图都是边长为6的正三角形,俯视图是直径等于6的圆,则这个空间几何体的表面积为( )
如图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称为左视图),其中正视图和侧视图都是边长为6的正三角形,俯视图是直径等于6的圆,则这个空间几何体的表面积为( )| A. | 18π | B. | 27π | C. | $\frac{82π}{3}$ | D. | $\frac{83π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (3,4) | C. | (2,4] | D. | (2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了制作广告牌,需在如图所示的铁片上切割出一个直角梯形,已知铁片由两部分组成,半径为1的半圆O及等腰直角三角形EFH,其中FE⊥FH.为裁剪出面积尽可能大的梯形铁片ABCD(不计损耗),将点A,B放在弧EF上,点C、D放在斜边EH上,且AD∥BC∥HF,设∠AOE=θ.
为了制作广告牌,需在如图所示的铁片上切割出一个直角梯形,已知铁片由两部分组成,半径为1的半圆O及等腰直角三角形EFH,其中FE⊥FH.为裁剪出面积尽可能大的梯形铁片ABCD(不计损耗),将点A,B放在弧EF上,点C、D放在斜边EH上,且AD∥BC∥HF,设∠AOE=θ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
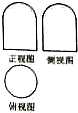 一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )| A. | 5π | B. | 6π | C. | 7π | D. | 9π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com