Question

已知f(x)＝x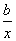＋－3，x∈[1，2]．

(1) 当b＝2时，求f(x)的值域；

(2) 若b为正实数，f(x)的最大值为M，最小值为m，且满足M－m≥4，求b的取值范围．

Answer 1

解：(1) 当b＝2时，f(x)＝x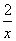＋－3，x∈[1，2]．

因为f(x)在[1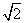，]上单调递减，在[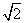，2]上单调递增，

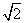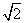所以f(x)的最小值为f()＝2－3.

又f(1)＝f(2)＝0，

所以f(x)的值域为[2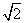－3，0]．

(2) ① 当0＜b＜2时，f(x)在[1，2]上单调递增，

则m＝b－2，M＝－1，此时M－m＝－＋1≥4，得b≤－6，与0＜b＜2矛盾，舍去；

② 当2≤b＜4时，f(x)在[1，]上单调递减，在[，2]上单调递增，所以M＝max{f(1)，f(2)}＝b－2，m＝f()＝2－3，则M－m＝b－2＋1≥4，得(－1)²≥4，解得b≥9，与2≤b＜4矛盾，舍去；

③ 当b≥4时，f(x)在[1，2]上单调递减，则M＝b－2，m＝－1，此时M－m＝－1≥4，得b≥10.综上所述，b的取值范围是[10，＋∞)．