练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．求证：（${C}_{n}^{0}$）2+（${C}_{n}^{1}$）2+…+（${C}_{n}^{n}$）2=${C}_{2n}^{n}$．

    分析 由（1+x）n（1+x）n=（1+x）2n，通过二项式定理，两边展开得，再根据组合数公式的性质，化简即可．

    解答 证明：由（1+x）n（1+x）n=（1+x）2n，两边展开得：
    （Cn0+Cn1x+Cn2x2+…+Cnm-1xn-1+Cnnxn）•（Cn0+Cn1x+Cn2x2+…+Cnn-1xn-1+Cnnxn）=C2n0+C2n1x+C2n1x2+…+C2n2nx2n
    比较等式两边xn的系数，它们应当相等，所以有：
    Cn0•Cnn+Cn1•Cnn-1+Cn2•Cnn-2+…+Cnn•Cn0=C2nn
    由Cnr=Cnn-r，
    得（Cn0）2+（Cn1）2+（Cn2）2+…+（Cnn）2=C2nn．

    点评 本题考查了组合及组合数公式，以及二项式展开定理，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．在数列{an}中，已知a1=2，a2=7，an+2等于anan+1（n∈N+）的个位数，则a2015=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知复数z：满足（1+$\sqrt{3}$i）z=1+i，则|z|等于（　　）
    A．$\frac{\sqrt{2}}{2}$B．-$\sqrt{2}$C．$\sqrt{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若两曲线y=x2与y=cx3（c＞0）所围成的图形面积为$\frac{2}{3}$，则c=（　　）
    A．$\frac{1}{3}$B．$\frac{1}{2}$C．1D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设函数f（x）=ax2+bx，g（x）=lnx，其中a，b为常数．
    （1）若a=0，且f（x）与g（x）相切，求b的值；
    （2）设函数h（x）=f（x）-g（x）．
    ①当b=0时，若h（x）≥0恒成立，求实数a的取值范围．
    ②若a+b=0，试讨论h（x）的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设集合M={x|x2-2x-3＜0，x∈Z}，则集合M的真子集个数为（　　）
    A．8B．7C．4D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

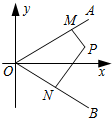    5．如图，射线OA，OB所在的直线的方向向量分别为$\overrightarrow{d_1}=（{1，k}）$，$\overrightarrow{d_2}=（{1，-k}）（{k＞0}）$，点P在∠AOB内，PM⊥OA于M，PN⊥OB于N；
    （1）若k=1，$P（{\frac{3}{2}，\frac{1}{2}}）$，求|OM|的值；
    （2）若P（2，1），△OMP的面积为$\frac{6}{5}$，求k的值；
    （3）已知k为常数，M，N的中点为T，且${S_{△MON}}=\frac{1}{k}$，当P变化时，求|OT|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知等比数列{bn}前n项和为Sn=3n-k，公差为k的等差数列{an}满足：b1=a1，求{an}，{bn}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知在直角梯形ABCD中，AB∥CD，AB⊥AD，AB=AD=2，CD=1，P为线段BC上一个动点，设$\overrightarrow{BP}=λ\overrightarrow{BC}$，则当$\overrightarrow{PA}•\overrightarrow{PD}$取得最小值时λ的值是（　　）
    A．$\frac{1}{2}$B．$\frac{4}{5}$C．0D．1

    查看答案和解析>>

    同步练习册答案