
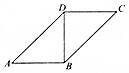
 如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm3.
如图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形ABCD,现将四边形ABCD沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的体积为500$\sqrt{3}$cm3. 分析 先确定三棱锥A-BCD的外接球直径为AC,再根据图中数据求出外接球的半径R,从而求得体积.
解答 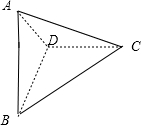 解:四边形ABCD中,∠ABD=∠BDC=90°,
解:四边形ABCD中,∠ABD=∠BDC=90°,
∴AB⊥BD,CD⊥BD;
∵沿BD折成直二面角A-BD-C,如图所示;
∴AB⊥平面BCD,CD⊥平面ABD,
∴AB⊥BC,CD⊥DA;
∴三棱锥A-BCD的外接球的直径为AC,
且|AC|2=|AB|2+|BD|2+|CD|2=102+102+102=300
∴外接球的半径为R=5$\sqrt{3}$,它的体积为$\frac{4π}{3}$•${(5\sqrt{3})}^{3}$=500$\sqrt{3}$π.
故答案为:500$\sqrt{3}$π.
点评 本题考查了几何体外接球的体积计算问题,解题的关键是确定外接球的直径.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $3\sqrt{2}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 40 | C. | 60 | D. | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com