
分析 (1)利用分析法证明即可,
(2)先放缩得到f(x)≤x+$\frac{1}{x+1}$,再构造函数g(x)=x+$\frac{1}{x+1}$,x∈[0,1],利用函数的单调性和最值得关系即可证明.
解答 证明:(1)由x∈[0,1],
则x+1∈[1,2],
要证f(x)≥1-x+x2,
只需证x3(x+1)+1≥(x+1)(1-x+x2),
只需证x4+x3+1≥x3+1,
只需证x4≥0,显然成立,
∴f(x)≥1-x+x2,
(2)∵0≤x≤1,∴x3≤x,
∴f(x)≤x+$\frac{1}{x+1}$,
设g(x)=x+$\frac{1}{x+1}$,x∈[0,1],
∴g′(x)=1-$\frac{1}{(x+1)^{2}}$=$\frac{{x}^{2}+2x}{(x+1)^{2}}$≥0,
∴g(x)在[0,1]上单调递增,
∴f(x)≤g(1)=$\frac{3}{2}$
点评 本题考查额分析法和导数和函数的单调性最值得关系,考查了分析问题,解决问题的能力,属于中档题


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -7 | C. | 12 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
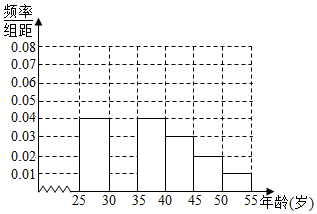
| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | q |
| 第六组 | [50,55) | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com