
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为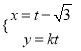 (
(![]() 为参数),直线
为参数),直线![]() 的参数程为
的参数程为 (
(![]() 为参数),设直线
为参数),设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时点
变化时点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为曲线
为曲线![]() 的动点,求点
的动点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,抛物线
,抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的上顶点,且
的上顶点,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影依次为
上的射影依次为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,当
,当![]() 变化时,证明:
变化时,证明: ![]() 为定值;
为定值;
(3)当![]() 变化时,直线
变化时,直线![]() 与
与![]() 是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.

(1)求频率分布直方图中a的值;
(2)估计总体中成绩落在[50,60)中的学生人数;
(3)根据频率分布直方图估计20名学生数学考试成绩的众数,平均数;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有四张卡片,每张卡片上写有一个数字,数字分别是![]() ,现从盒子中随机抽取卡片,每张卡片被抽到的概率相等.
,现从盒子中随机抽取卡片,每张卡片被抽到的概率相等.
(1)若一次抽取三张卡片,求抽到的三张卡片上的数字之和大于![]() 的概率;
的概率;
(2)若第一次抽一张卡片,放回后搅匀再抽取一张卡片,求两次抽取中至少有一次抽到写有数字![]() 的卡片的概率.
的卡片的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 轴被曲线
轴被曲线![]() 截得的线段长等于
截得的线段长等于![]() 的长半轴长。
的长半轴长。
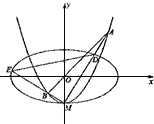
(1)求![]() ,
, ![]() 的方程;
的方程;
(2)设![]() 与
与![]() 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线![]() 与
与![]() 相交于点A,B,直线MA,MB分别与
相交于点A,B,直线MA,MB分别与![]() 相交与D,E.
相交与D,E.
①证明: ![]() ;
;
②记△MAB,△MDE的面积分别是![]() .问:是否存在直线
.问:是否存在直线![]() ,使得
,使得![]() =
=![]() ?请说明理由。
?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔,唐三彩的生产至今已有1300多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史。某陶瓷厂在生产过程中,对仿制的100件工艺品测得其重量(单位; ![]() )数据,将数据分组如下表:
)数据,将数据分组如下表:
分组 | 频数 | 频率 |
| 4 | |
| 26 | |
| ||
| 28 | |
| 10 | |
| 2 | |
合计 | 100 |
(1)在答题卡上完成频率分布表;
(2)以表中的频率作为概率,估计重量落在![]() 中的概率及重量小于2.45的概率是多少?
中的概率及重量小于2.45的概率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() 作为代表.据此,估计这100个数据的平均值.
作为代表.据此,估计这100个数据的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() 内一定点
内一定点![]() ,动圆
,动圆![]() 过点
过点![]() 且与圆
且与圆![]() 内切.记动圆圆心
内切.记动圆圆心![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求轨迹![]() 方程;
方程;
(II)过点![]() 的动直线l交轨迹
的动直线l交轨迹![]() 于M,N两点,试问:在坐标平面上是否存在一个定点Q,使得以线段MN为直径的圆恒过点Q?若存在,求出点Q的坐标;若不存在,请说明理由.
于M,N两点,试问:在坐标平面上是否存在一个定点Q,使得以线段MN为直径的圆恒过点Q?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届河南省南阳市第一中学高三上学期第八次考试】2017年5月14日至15日,“一带一路”国际合作高峰论坛在中国首都北京举行,会议期间,达成了多项国际合作协议.假设甲、乙两种品牌的同类产品出口某国家的市场销售量相等,该国质量检验部门为了解他们的使用寿命,现从这两种品牌的产品中分别随机抽取300个进行测试,结果统计如下图所示.
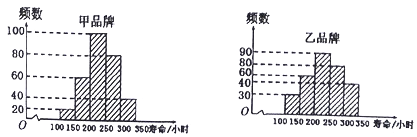
(1)估计甲品牌产品寿命小于200小时的概率;
(2)在抽取的这两种品牌产品中,抽取寿命超过300小时的产品3个,设随机变量![]() 表示抽取的产品是甲品牌的产品个数,求
表示抽取的产品是甲品牌的产品个数,求![]() 的分布列和数学期望值.
的分布列和数学期望值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com