
分析 (1)利用两角和差的正弦公式化简条件可得4cos(α+β)sinα=2sin(α+β)cosα,从而证得要证得等式成立.
(2)由条件根据tanβ=tan[(α+β)-α],利用两角差的正切公式,求得函数f(x)的解析式.
(3)利用条件可得0<α<$\frac{π}{3}$,tanα∈(0,$\sqrt{3}$),即x∈(0,$\sqrt{3}$),由此求得函数f(x)=$\frac{x}{1+{2x}^{2}}$=$\frac{1}{\frac{1}{x}+2x}$,利用基本不等式以及函数的单调性,求得函数f(x)的值域.
解答 解:(1)证明:∵sin(2α+β)=3sinβ,∴sin[(α+β)+α]=3sin[(α+β)-α],
展开可得sin(α+β)cosα+cos(α+β)sinα=3sin(α+β)cosα-3cos(α+β)sinα,
4cos(α+β)sinα=2sin(α+β)cosα,∴tan(α+β)=2tanα.
(2)∵tanα=x,tanβ=y,y=f(x),
又tanβ=tan[(α+β)-α]=$\frac{tan(α+β)-tanα}{1+tan(α+β)tanα}$=$\frac{2tanα-tanα}{1+2tanα•tanα}$=$\frac{x}{1+{2x}^{2}}$,
即函数f(x)的解析式y=f(x)=$\frac{x}{1+{2x}^{2}}$.
(3)若角α是一个三角形的最小内角,则0<α<$\frac{π}{3}$,tanα∈(0,$\sqrt{3}$),即x∈(0,$\sqrt{3}$),
则函数f(x)=$\frac{x}{1+{2x}^{2}}$=$\frac{1}{\frac{1}{x}+2x}$≤$\frac{1}{2\sqrt{2}}$=$\frac{\sqrt{2}}{4}$,当且仅当x=$\frac{\sqrt{2}}{2}$时,取等号.
函数f(x)在(0,$\frac{\sqrt{2}}{2}$)上单调递增,在($\frac{\sqrt{2}}{2}$,$\sqrt{3}$)上单调递减,
当x趋于零时,f(x))=$\frac{x}{1+{2x}^{2}}$ 趋于0,当x趋于$\sqrt{3}$时,f(x))=$\frac{x}{1+{2x}^{2}}$ 趋于$\frac{\sqrt{3}}{7}$,
故函数f(x)的值域为(0,$\frac{\sqrt{2}}{4}$].
点评 本题主要考查两角和差的正弦、正切公式的应用,求函数的解析式,基本不等式的应用,求函数的值域,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
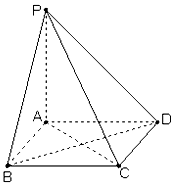 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 |
| A. | 增加0.9个单位 | B. | 减少0.9个单位 | C. | 增加0.72个单位 | D. | 减少0.72个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com