
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,e) | D. | (e,4) |
分析 利用换元法求出函数f(x)的解析式,然后根据函数与方程的关系进行转化,构造函数,判断函数的零点即可得到结论.
解答 解:∵f(x)是定义在(0,+∞)上单调函数,且对?x∈(0,+∞),都有f(f(x)-lnx)=e+1,
∴设f(x)-lnx=t,则f(t)=e+1,
即f(x)=lnx+t,
令x=t,则f(t)=lnt+t=e+1,
则t=e,
即f(x)=lnx+e,
函数的导数f′(x)=$\frac{1}{x}$,
则由f(x)-f′(x)=e得lnx+e-$\frac{1}{x}$=e,
即lnx-$\frac{1}{x}$=0,
设h(x)=lnx-$\frac{1}{x}$,
则h(1)=ln1-1=-1<0,h(e)=lne-$\frac{1}{e}$=1-$\frac{1}{e}$>0,
∴函数h(x)在(1,e)上存在一个零点,即方程f(x)-f′(x)=e的实数解所在的区间是(1,e),
故选:C.
点评 本题主要考查函数与方程的应用,根据函数单调性的性质,利用换元法求出函数的解析式是解决本题的关键.综合性较强,涉及的知识点较多.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | 3 | C. | 4 | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,$\frac{1}{2e}$) | C. | (-∞,0)∪($\frac{1}{2e}$,+∞) | D. | ($\frac{1}{2e}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
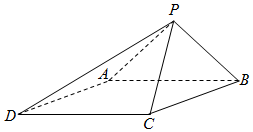 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{7}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,有一个底面是正方形的直棱柱型容器(无盖),底面棱长为1dm(dm为分米),高为5dm,两个小孔在其相对的两条侧棱上,且到下底面距离分别为3dm和4dm,则(水不外漏情况下)此容器可装的水最多为( )
如图,有一个底面是正方形的直棱柱型容器(无盖),底面棱长为1dm(dm为分米),高为5dm,两个小孔在其相对的两条侧棱上,且到下底面距离分别为3dm和4dm,则(水不外漏情况下)此容器可装的水最多为( )| A. | $\frac{9}{2}d{m^3}$ | B. | 4dm3 | C. | $\frac{7}{2}d{m^3}$ | D. | 3dm3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com