练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中，
    AD
    =2
    DC
    ，
    BA
    =
    a
    ，
    BD
    =
    b
    ，
    BC
    =
    c
    ，则下列等式成立的是（　　）
    A、
    c
    =2
    b
    -
    a
    B、
    c
    =2
    a
    -
    b
    C、
    c
    =
    3
    a
    2
    -
    b
    2
    D、
    c
    =
    3
    b
    2
    -
    a
    2
    考点：向量加减混合运算及其几何意义
    专题：平面向量及应用
    分析：利用向量的三角形法则即可得出．
    解答： 解：如图所示，
    ∵
    AD
    =
    AB
    +
    BD
    ，
    DC
    =
    DB
    +
    BC
    ，
    AD
    =2
    DC
    ，
    ∴
    AB
    +
    BD
    =2(
    DB
    +
    BC
    )    ，
    ∴-
    a
    +
    b
    =2(-
    b
    +
    c
    )    ，
    化为
    c
    =
    3
    2
    b
    -
    1
    2
    a
    ．
    故选：D．
    点评：本题考查了向量的三角形法则，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

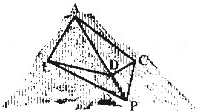    某度假区以2014年索契冬奥会为契机，依山修建了高山滑雪场．为了适应不同人群的需要，从山上A处到山脚滑雪服务区P处修建了滑雪赛道A-C-P和滑雪练习道A-E-P（如图）．已知cos∠ACP=一
    		5
    5
    ，cos∠APC=
    4
    5
    ，cos∠APE=
    2
    3
    ，公路AP长为10（单位：百米），滑道EP长为6（单位：百米）．
    （Ⅰ）求滑道CP的长度；
    （Ⅱ）由于C，E处是事故的高发区，为及时处理事故，度假区计划在公路AP上找一处D，修建连接道
    DC，DE，问DP多长时，才能使连接道DC+DE最短，最短为多少百米？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a＞0，b＞0，方程为x2+y2-4x+2y=0的曲线关于直线ax-by-1=0对称，则
    3a+2b
    ab
    的最小值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    直线x+y=
    		2
    与两坐标轴围成的三角形区域为D，在D内任取一点P（x，y），那么使得x2+y2≤1的概率为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=|x-a|（a∈R）．
    （Ⅰ）若a=2，求不等式f（x）＜1的解集；
    （Ⅱ）若不等式f（x）+|x+1|≥3在R上恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    向边长分别为5，6，
    		13
    的三角形区域内随机投一点M，则该点M与三角形三个顶点距离都大于1的概率为（　　）
    A、1-
    π
    18
    B、1-
    π
    12
    C、1-
    π
    9
    D、1-
    π
    4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若集合A={1，m2}，集合B={3，9}，则“m=3”是“A∩B={9}”的（　　）
    A、充分不必要条件
    B、必要不充分条件
    C、充分必要条件
    D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    从[0，10]中任取一个数x，从[0，6]中任取一个数y，则使|x-5|+|y-3|≤4的概率为（　　）
    A、
    1
    2
    B、
    5
    9
    C、
    2
    3
    D、
    5
    12

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面关于f（x）的判断：
    ①y=f（x-2）与y=f（2-x）的图象关于直线x=2对称；
    ②若f（x）为偶函数，且f（2+x）=-f（x），则f（x）的图象关于直线x=2对称．
    ③设函数f（x）=lnx，且x0，x1，x2∈（0，+∞），若x1＜x2，则
    1
    x2
    ＞
    f(x1)-f(x2)
    x1-x2
    ．
    ④函数f（x）=lnx，x0，x1，x2∈（0，+∞），存在x0∈（x1，x2），（x1＜x2），使得
    1
    x0
    =
    f(x1)-f(x2)
    x1-x2
    ．
    ⑤设函数f（x）=x2-3x+4，g(x)=
    1
    2
    x2+4lnx+a    ．对于?x1∈[1，e]，总?x2∈[1，e]，使得f（x1）=g（x2），则实数a的取值范围为[1，
    5
    4
    ]    ．
    其中正确的判断是
     
    （把你认为正确的判断都填上）

    查看答案和解析>>

    同步练习册答案