
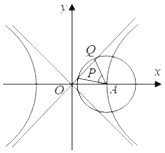
 如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点为A,O 为坐标原点,以A 为圆心的圆与双曲线C 的一条渐近线交于 P,Q 两点.若∠PAQ=60°,且|PQ|=$\frac{{\sqrt{3}}}{3}a$,则双曲线C 的渐近线方程为( )
如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点为A,O 为坐标原点,以A 为圆心的圆与双曲线C 的一条渐近线交于 P,Q 两点.若∠PAQ=60°,且|PQ|=$\frac{{\sqrt{3}}}{3}a$,则双曲线C 的渐近线方程为( )| A. | $y=±\frac{{\sqrt{3}}}{3}x$ | B. | $y=±\frac{{\sqrt{3}}}{2}x$ | C. | y=±3x | D. | $y=±\frac{{2\sqrt{3}}}{3}x$ |
分析 确定△QAP为等边三角形,A到渐近线的距离=$\frac{b}{\sqrt{\frac{{b}^{2}}{{a}^{2}}+1}}$=$\frac{\sqrt{3}}{2}•$$\frac{{\sqrt{3}}}{3}a$,即可得出结论.
解答 解:因为∠PAQ=60°,所以△QAP为等边三角形,
渐近线方程为y=$\frac{b}{a}$x,A(a,0),A到渐近线的距离=$\frac{b}{\sqrt{\frac{{b}^{2}}{{a}^{2}}+1}}$=$\frac{\sqrt{3}}{2}•$$\frac{{\sqrt{3}}}{3}a$,
所以3b2=a2,
∴$\frac{b}{a}$=$\frac{\sqrt{3}}{3}$,可得双曲线C 的渐近线方程为y=$±\frac{\sqrt{3}}{3}$x.
故选:A.
点评 本题考查双曲线的性质,考查点到直线距离公式的运用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| B. | 若p且q为假命题,则p,q均为假命题 | |
| C. | “x=-1”是“x2-5x-6=0”的充分不必要条件 | |
| D. | 命题p:存在x0∈R,使得x02+x0+1<0,则非p:任意x∈R,都有x2+x+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.352 | B. | 0.432 | C. | 0.36 | D. | 0.648 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ①③④ | C. | ②④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
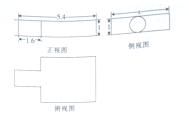 中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中x的为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中x的为( )| A. | 2.5 | B. | 3 | C. | 3.2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com