
| A�� | �٢ڢ� | B�� | �٢ۢ� | C�� | �ڢ� | D�� | �ڢ� |
���� ���ݳ�Ҫ�����Ķ��壬���жϢ٣�д��ԭ����ķ����жϢڣ����ݸ�����������жϵ���ֵ�������жϢۣ�д��ԭ����������⣬���жϢܣ�
��� �⣺����֪m��n�dz�������mn��0���ǡ�mx2+ny2=1��ʾ˫���ߵij�Ҫ���������ʢٴ���
������p����?x��R��sinx��1���ķ��ǩVp����?x0��R��sinx0��1�����ʢ���ȷ��
����֪����p��q����p��q�Ǽ����⣬��p��q��Ϊ�����⣬�ʢ۴���
�����⡰��a��b��0����a2��b2���������������⡰��a2��b2����a��b��0�����Ǽ����⣬�ʢ���ȷ��
��ѡ��C
���� ���������������ж���Ӧ��Ϊ���壬�����˳�Ҫ����������ķ��������⣬�������⣬�ѶȻ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{5}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
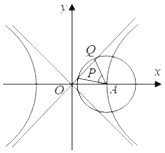 ��ͼ����֪˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��a��0��b��0��$���Ҷ���ΪA��O Ϊ����ԭ�㣬��A ΪԲ�ĵ�Բ��˫����C ��һ�������߽��� P��Q ���㣮����PAQ=60�㣬��|PQ|=$\frac{{\sqrt{3}}}{3}a$����˫����C �Ľ����߷���Ϊ��������
��ͼ����֪˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��a��0��b��0��$���Ҷ���ΪA��O Ϊ����ԭ�㣬��A ΪԲ�ĵ�Բ��˫����C ��һ�������߽��� P��Q ���㣮����PAQ=60�㣬��|PQ|=$\frac{{\sqrt{3}}}{3}a$����˫����C �Ľ����߷���Ϊ��������| A�� | $y=��\frac{{\sqrt{3}}}{3}x$ | B�� | $y=��\frac{{\sqrt{3}}}{2}x$ | C�� | y=��3x | D�� | $y=��\frac{{2\sqrt{3}}}{3}x$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 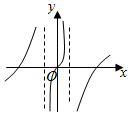 | C�� | 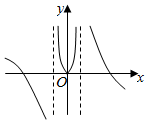 | D�� | 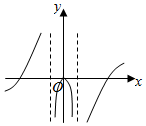 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
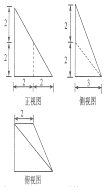
| A�� | 8 | B�� | 10 | C�� | 12 | D�� | 14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com