
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
分析 可知$|\overrightarrow{a}|=|\overrightarrow{b}|=1,<\overrightarrow{a},\overrightarrow{b}>=60°$,进行数量积的运算即可由$\overrightarrow{b}•[(1-t)\overrightarrow{a}+t\overrightarrow{b}]=-\frac{1}{2}$得出关于t的方程,解出t即可.
解答 解:
$\overrightarrow{b}•\overrightarrow{c}=\overrightarrow{b}•[(1-t)\overrightarrow{a}+t\overrightarrow{b}]$
=$(1-t)\overrightarrow{b}•\overrightarrow{a}+t{\overrightarrow{b}}^{2}$
=$\frac{1-t}{2}+t$
=$-\frac{1}{2}$;
解得t=-2.
故选D.
点评 考查单位向量的概念,向量数量积的运算及计算公式.


科目:高中数学 来源: 题型:填空题
 体积为18$\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是[8π,16π].
体积为18$\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是[8π,16π].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
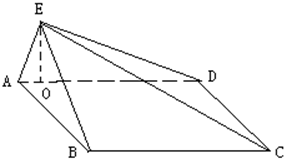 如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.
如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{π}$ | B. | $\frac{{6\sqrt{3}}}{π}$ | C. | $\frac{4}{3}$ | D. | $\frac{{4\sqrt{3}}}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[2,\frac{5}{2}]$ | B. | [4,6] | C. | $[\frac{119}{25},\frac{48}{5}]$ | D. | $[\frac{144}{25},\frac{53}{5}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com