
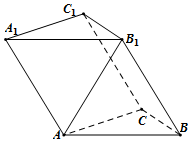
 如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.
如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.分析 (Ⅰ)设AB中点为O,连OC,OB1,B1C,则截面OB1C为所求,通过证明AB⊥OC,AB⊥OB1,推出AB⊥平面OB1C.
(Ⅱ)以O为原点,OB方向为x轴方向建立如图所示的空间直角坐标系,求出平面BCC1B1的一个法向量,入会利用空间向量的数量积求解AC1与平面BCC1B1所成角的正弦值.
解答 解:(Ⅰ)设AB中点为O,连OC,OB1,B1C,则截面OB1C为所求,…(3分)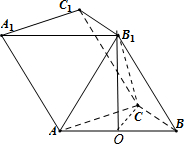
证明:OC,OB1分别为△ABC,△ABB1的中线,所以AB⊥OC,AB⊥OB1,
又OC,OB1为平面OB1C内的两条相交直线,所以AB⊥平面OB1C,…(6分)
(Ⅱ)以O为原点,OB方向为x轴方向建立如图所示的空间直角坐标系,
易求得B(1,0,0),A(-1,0,0),$C(0,\sqrt{3},0),{B_1}(0,0,\sqrt{3}),{C_1}(-1,\sqrt{3},\sqrt{3})$$\overrightarrow{CB}=(1,-\sqrt{3},0),\overrightarrow{{B_1}B}=(1,0,-\sqrt{3}),\overrightarrow{A{C_1}}=(0,\sqrt{3},\sqrt{3})$,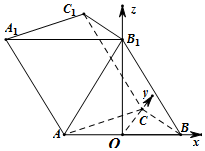
…(8分)
设平面BCC1B1的一个法向量为$\overrightarrow n=(x,y,z)$,
由$\left\{\begin{array}{l}\overrightarrow n⊥\overrightarrow{CB}\\ \overrightarrow n⊥\overrightarrow{{B_1}B}\end{array}\right.?\left\{\begin{array}{l}x-\sqrt{3}y=0\\ x-\sqrt{3}z=0\end{array}\right.$解得平面BCC1B1的一个法向量为$\overrightarrow n=(\sqrt{3},1,1)$,…(10分)
$|cos<\overrightarrow{A{C_1}},\overrightarrow n>|=\frac{{|\overrightarrow{A{C_1}}•\overrightarrow n|}}{{|\overrightarrow{A{C_1}}|•|\overrightarrow n|}}=\frac{{\sqrt{3}+\sqrt{3}}}{{\sqrt{6}•\sqrt{5}}}=\frac{{\sqrt{10}}}{5}$,
所以AC1与平面BCC1B1所成角的正弦值为$\frac{{\sqrt{10}}}{5}$…(12分)
点评 本题考查直线与平面垂直,直线与平面所成角的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,2] | B. | ($\frac{1}{2}$,2] | C. | [$\frac{1}{2}$,2) | D. | ($\frac{1}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 14 | C. | 15或16 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22018-1 | B. | 22018+1 | C. | 22017-1 | D. | 22017+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | 5π | C. | 10π | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com