
分析 问题转化为a( $\frac{1+lnx}{x}$-e)min对于任意x∈[$\frac{1}{e}$,2]恒成立,设f(x)=$\frac{1+lnx}{x}$-e,求出函数f(x)的最小值即可求出a的最大值.
解答 解:(a+e)x-1-lnx≤0对于任意x∈[$\frac{1}{e}$,2]恒成立
?a≤$\frac{1+lnx}{x}$-e对于任意x∈[$\frac{1}{e}$,2]恒成立
?a≤( $\frac{1+lnx}{x}$-e)min对于任意x∈[$\frac{1}{e}$,2]恒成立
设f(x)=$\frac{1+lnx}{x}$-e,x∈[$\frac{1}{e}$,2],则f′(x)=-$\frac{lnx}{{x}^{2}}$,
令f′(x)>0,解得:$\frac{1}{e}$≤x<1,令f′(x)>0,解得:1<x≤2,
∴f(x)在[$\frac{1}{e}$,1)递增,在(1,2]递减,
∴f($\frac{1}{e}$)或f(2)最小,
而f($\frac{1}{e}$)=-e,f(2)=$\frac{1}{2}$(1+ln2)-e,
∴f($\frac{1}{e}$)<f(2),
∴a的最大值是-e,
故答案为:-e.
点评 本题考查函数恒成立问题,着重考查构造函数思想、等价转化思想与导数法求极值的综合应用,求得f(x)的最小值是关键,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
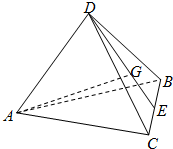 如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为△DBC的重心,则AG=$\frac{\sqrt{23}}{3}$.
如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为△DBC的重心,则AG=$\frac{\sqrt{23}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 色盲 | 不色盲 | 合计 | |
| 男 | 38 | 442 | 480 |
| 女 | 6 | 514 | 520 |
| 合计 | 44 | 956 | 1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 图中的三个正方形块中,着色的正方形的个数依次构成一个数列{an},根据着色的规律,则a4=585,数列{an}的通项公式an=$\frac{{8}^{n}-1}{7}$.
图中的三个正方形块中,着色的正方形的个数依次构成一个数列{an},根据着色的规律,则a4=585,数列{an}的通项公式an=$\frac{{8}^{n}-1}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com