
分析 ${log_2}{a_{n+1}}+{log_2}{a_n}=n(n∈{N^*})$,可得anan+1=2n.可得$\frac{{a}_{n+2}}{{a}_{n}}$=2.数列{an}的奇数项与偶数项分别成等比数列,公比为2,首项分别为1,2.利用等比数列的求和公式即可得出.
解答 解:∵${log_2}{a_{n+1}}+{log_2}{a_n}=n(n∈{N^*})$,
∴anan+1=2n.
∴$\frac{{a}_{n+1}{a}_{n+2}}{{a}_{n}{a}_{n+1}}$=$\frac{{2}^{n+1}}{{2}^{n}}$,可得$\frac{{a}_{n+2}}{{a}_{n}}$=2.
∴数列{an}的奇数项与偶数项分别成等比数列,公比为2,首项分别为1,2.
则${a_1}+{a_2}+…{a_{2017}}-{2^{1010}}$=(a1+a3+…+a2017)+(a2+a4+…+a2016)-21010
=$\frac{{2}^{1009}-1}{2-1}$+$\frac{2({2}^{1008}-1)}{2-1}$-21010=-3.
故答案为:-3.
点评 本题考查了等比数列的通项公式与求和公式、分组求和方法、对数运算性质,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
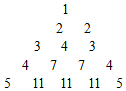 观察如图所示的”三角数阵”
观察如图所示的”三角数阵”查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 圆台侧面的母线长为2a,母线与轴的夹角为30°,一个底面的半径是另一个底面半径的2倍.求两底面的面积之和是( )
圆台侧面的母线长为2a,母线与轴的夹角为30°,一个底面的半径是另一个底面半径的2倍.求两底面的面积之和是( )| A. | 3πa2 | B. | 4πa2 | C. | 5πa2 | D. | 6πa2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》有如下问题:有上禾三秉(古代容量单位),中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾一秉各几何?依上文:设上、中、下禾一秉分别为x斗、y斗、z斗,设计如图所示的程序框图,则输出的x,y,z的值分别为( )
《九章算术》有如下问题:有上禾三秉(古代容量单位),中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾一秉各几何?依上文:设上、中、下禾一秉分别为x斗、y斗、z斗,设计如图所示的程序框图,则输出的x,y,z的值分别为( )| A. | $\frac{37}{4},\frac{17}{4},\frac{11}{4}$ | B. | $\frac{11}{4},\frac{37}{4},\frac{17}{4}$ | C. | $\frac{35}{4},\frac{17}{4},\frac{9}{4}$ | D. | $\frac{35}{4},\frac{9}{4},\frac{17}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| PM2.5 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 重度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 15 | 18 | 30 | 7 | 11 | 15 |
| P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.32 | 2.07 | 2.70 | 3.841 | 5.02 | 6.63 | 7.87 | 10.828 |
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com