
| A. | 2x-y-3=0 | B. | 2x+y-3=0 | C. | x-2y-3=0 | D. | x+2y-3=0 |
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或$\frac{1}{4}$ | B. | $\frac{1}{2}$或$\frac{1}{8}$ | C. | 1或$\frac{1}{2}$ | D. | 1或$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
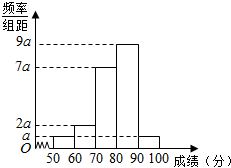 某中学举行电脑知识竞赛,对40名参赛选手考试成绩(单位:分)进行统计,发现他们的成绩分布在[50,60),[60,70),[70,80),[90,100),并得到如图所示的频率分布直方图
某中学举行电脑知识竞赛,对40名参赛选手考试成绩(单位:分)进行统计,发现他们的成绩分布在[50,60),[60,70),[70,80),[90,100),并得到如图所示的频率分布直方图查看答案和解析>>
科目:高中数学 来源: 题型:解答题
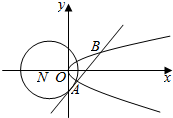 已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x(月份) | 1 | 2 | 3 | 4 | 5 | 6 |
| Q(x)(台) | 6 | 9 | 10 | 8 | 6 | 2 |
| A. | Q(x)=ax+b(a≠0) | B. | Q(x)=a|x-4|+b(a≠0) | ||
| C. | Q(x)=a(x-3)2+b(a≠0) | D. | Q(x)=a•bx(a≠0,b>0且b≠1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | $({0,\frac{1}{2}})$ | C. | $({0,\frac{1}{4}})$ | D. | $({0,\frac{1}{8}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com