
|
|


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
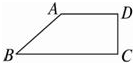 一个水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )
一个水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( ) A、
| ||||||
B、2+
| ||||||
C、
| ||||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| b-a |
| c |
| sinB-sinC |
| sinB+sinA |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 10 |
| 1 |
| 5 |
| 7 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 5 |
| 6 |
| 25 |
| 3 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 120000 |
| 1 |
| 50 |
| 18 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
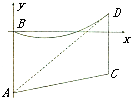 在一段笔直的斜坡AC上竖立两根高16米的电杆AB,CD,过B,D架设一条10万伏高压电缆线.假设电缆线BD呈抛物线形状,现以B为原点,AB所在直线为Y轴建立如图所示的平面直角坐标系,经观测发现视线AD恰与电缆线相切于点D(m,n).
在一段笔直的斜坡AC上竖立两根高16米的电杆AB,CD,过B,D架设一条10万伏高压电缆线.假设电缆线BD呈抛物线形状,现以B为原点,AB所在直线为Y轴建立如图所示的平面直角坐标系,经观测发现视线AD恰与电缆线相切于点D(m,n).查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| OA |
| OM |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com