
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
科目:高中数学 来源: 题型:解答题
 四棱锥P-ABCD的底面ABCD是平行四边形,PA=AD,M,N分别是棱PC,AB的中点,且MN⊥CD.
四棱锥P-ABCD的底面ABCD是平行四边形,PA=AD,M,N分别是棱PC,AB的中点,且MN⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我市湘阴县地处长沙北部、南洞庭湖滨,是长株潭“两型社会”综合配套改革试验区核心区--滨湖示范区的重要组成部分,是全省承接产业发展加工贸易试点县和全省最具投资吸引力的五个县之一.在市委市政府的指导下,计划于2015年在湘阴县长湘公路一侧建设一新型工业园.利用已有地形,现拟在乡村公路上某处C到长湘公路某处B新建一条长为$\sqrt{3}$公里的公路,围成一个三角形区域建设工业园(如图所示).已知∠A=60°.
我市湘阴县地处长沙北部、南洞庭湖滨,是长株潭“两型社会”综合配套改革试验区核心区--滨湖示范区的重要组成部分,是全省承接产业发展加工贸易试点县和全省最具投资吸引力的五个县之一.在市委市政府的指导下,计划于2015年在湘阴县长湘公路一侧建设一新型工业园.利用已有地形,现拟在乡村公路上某处C到长湘公路某处B新建一条长为$\sqrt{3}$公里的公路,围成一个三角形区域建设工业园(如图所示).已知∠A=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
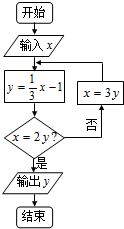
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,e2] | B. | [0,e2) | C. | [0,e4] | D. | [0,e4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com