
| A. | 18 | B. | 14 | C. | 30 | D. | 34 |
分析 作出图形,求出二面角的大小,EC,AE,AC,使用余弦定理求出$\overrightarrow{AE},\overrightarrow{AC}$的夹角,代入数量积公式计算.
解答 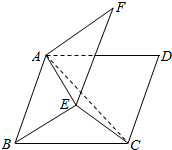 解:∵$\overrightarrow{AD}$•$\overrightarrow{AF}$=4×4×cos∠DAF=2,∴cos∠DAF=$\frac{1}{8}$.∴cos∠CBE=cos∠DAF=$\frac{1}{8}$.
解:∵$\overrightarrow{AD}$•$\overrightarrow{AF}$=4×4×cos∠DAF=2,∴cos∠DAF=$\frac{1}{8}$.∴cos∠CBE=cos∠DAF=$\frac{1}{8}$.
∴CE=$\sqrt{B{C}^{2}+B{E}^{2}-2BC•BEcos∠CBE}$=2$\sqrt{7}$.
∵AC=AE=4$\sqrt{2}$,∴cos∠CAE=$\frac{A{C}^{2}+A{E}^{2}-C{E}^{2}}{2AC•AE}$=$\frac{9}{16}$.
∴$\overrightarrow{AC}$•$\overrightarrow{AE}$=AC•AE•cos∠CAE=4$\sqrt{2}$×4$\sqrt{2}$×$\frac{9}{16}$=18.
故选:A.
点评 本题考查了平面向量的数量积运算,余弦定理的应用,属于中档题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 都大于2 | B. | 至少有一个不大于2 | ||
| C. | 都小于2 | D. | 至少有一个不小于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲正确乙错误 | B. | 甲错误乙正确 | C. | 甲错误乙也错误 | D. | 甲正确乙也正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 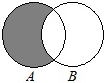 | B. | 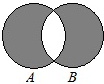 | C. | 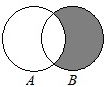 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=4 | B. | m=0 | C. | m=4或m=-4 | D. | m=4且n≠-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com