
分析 (1)利用诱导公式化简函数f(x)的解析式.
(2)利用诱导公式化简f(α)=f(-18600)的值,可得结果.
(3)利用同角三角的基本关系求得cos(α-$\frac{π}{6}$)的值,再利用两角和差的余弦公式,求得f(α)的值.
解答 解:(1)f(α)=$\frac{{sin(\frac{π}{2}-α)cos(10π-α)tan(-α+3π)}}{{tan(π+α)sin(\frac{5π}{2}+α)}}$=$\frac{cosα•cosα•(-tanα)}{tanα•cosα}$=-cosα.
(2)∵α=-18600=-6×3600+3000,∴f(α)=f(-18600)=-cos(-18600)=$-cos(-6×{360^0}+{300^0})=-cos{60^0}=-\frac{1}{2}$.
(3)∵$α∈(0,\frac{π}{2}),sin(α-\frac{π}{6})=\frac{1}{3}∴cos(α-\frac{π}{6})=\frac{{2\sqrt{2}}}{3}$,
∴f(α)=-cosα=-cos[(α-$\frac{π}{6}$)+$\frac{π}{6}$]=-cos(α-$\frac{π}{6}$)cos$\frac{π}{6}$+sin(α-$\frac{π}{6}$)sin$\frac{π}{6}$=-$\frac{2\sqrt{2}}{3}$•$\frac{\sqrt{3}}{2}$+$\frac{1}{3}•\frac{1}{2}$=$\frac{1-2\sqrt{6}}{6}$.
点评 本题主要考查诱导公式的应用,两角和差的余弦公式,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
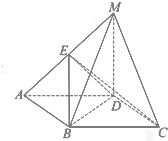 如图,四棱锥M-ABCD中,底面ABCD为矩形,MD⊥平面ABCD,且MD=DA=1,E为MA中点.
如图,四棱锥M-ABCD中,底面ABCD为矩形,MD⊥平面ABCD,且MD=DA=1,E为MA中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 优秀 | 不优秀 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|a≤2} | B. | {a|a≤1} | C. | {a|a≥1} | D. | {a|a≥2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com