
分析 已知等式利用诱导公式化简求出cosα的值,根据α的范围,利用同角三角函数间的基本关系求出sinα与tanα的值即可.
解答 解:∵sin(α-$\frac{π}{2}$+4kπ)=sin(α-$\frac{π}{2}$)=-cosα=$\frac{1}{3}$,k∈Z且α∈(π,$\frac{3π}{2}$),
∴cosα=-$\frac{1}{3}$,sinα=-$\sqrt{1-co{s}^{2}α}$=-$\frac{2\sqrt{2}}{3}$,tanα=$\frac{sinα}{cosα}$=2$\sqrt{2}$.
点评 此题考查了运用诱导公式化简求值,以及同角三角函数间的基本关系,熟练掌握诱导公式是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD是平行四边形,E为PD的中点,点F在棱PD上,且FD=$\frac{1}{3}$PD.
在四棱锥P-ABCD中,底面ABCD是平行四边形,E为PD的中点,点F在棱PD上,且FD=$\frac{1}{3}$PD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,EA=ED,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,EA=ED,AE⊥平面CDE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
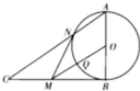 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作圆O与斜边AB交于N,过点O作OM∥AC,交BC于M,交圆O于Q.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径作圆O与斜边AB交于N,过点O作OM∥AC,交BC于M,交圆O于Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{2\sqrt{3}}{9}$) | C. | (0,$\frac{\sqrt{3}}{3}$) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=60°,AB=2AD,PD⊥平面ABCD,点M为PC上的点,且PM=2MC.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=60°,AB=2AD,PD⊥平面ABCD,点M为PC上的点,且PM=2MC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com