
| A. | a=b<c | B. | a=b>c | C. | b=c<a | D. | b=c>a |
分析 利用对数的运算性质分别化简a,b,c,再利用不等式的性质、对数函数的单调性即可判断出大小关系.
解答 解:∵f(x)=lnx,0<x1<x2,
∴函数f(x)在(0,+∞)上单调递增.
$a=f(\sqrt{{x_1}{x_2}})$=$ln\sqrt{{x}_{1}{x}_{2}}$,$b=\frac{1}{2}(f({x_1})+f({x_2}))$=$\frac{1}{2}(ln{x}_{1}+ln{x}_{2})$=$ln\sqrt{{x}_{1}{x}_{2}}$,$c=f(\frac{{{x_1}+{x_2}}}{2})$=$ln\frac{{x}_{1}+{x}_{2}}{2}$>$ln\sqrt{{x}_{1}{x}_{2}}$,
∴a=b<c.
故选:A.
点评 本题考查了不等式的性质、对数函数的单调性及其运算法则,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{{\sqrt{2}}}{2}]$ | B. | $[\frac{{\sqrt{2}}}{2},+∞)$ | C. | $[-\frac{1}{2},\frac{1}{2}]$ | D. | $[-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{π}{3},\frac{2π}{3}}]$ | B. | $[{\frac{π}{6},\frac{5π}{6}}]$ | C. | $({0,\frac{π}{3}}]∪[{\frac{2π}{3},π})$ | D. | $[{\frac{π}{3},\frac{π}{2}})∪({\frac{π}{2},\frac{2π}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
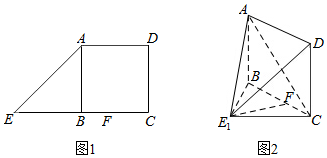 如图1,在直角梯形ADCE中,AD∥EC,EC=2BC,∠ADC=90°,AB⊥EC,点F为线段BC上的一点.将△ABE沿AB折到△ABE1的位置,使E1F⊥BC,如图2.
如图1,在直角梯形ADCE中,AD∥EC,EC=2BC,∠ADC=90°,AB⊥EC,点F为线段BC上的一点.将△ABE沿AB折到△ABE1的位置,使E1F⊥BC,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com