
分析 根据函数奇偶性的性质将不等式进行转化即可.
解答 解:由题意,奇函数f(x)是定义在[-1,1]上的减函数,不等式f(1-m)+f(1-m2)<0,
即f(1-m)<f(m2-1),
则$\left\{\begin{array}{l}{-1≤1-m≤1}\\{-1≤1-{m}^{2}≤1}\\{1-m>{m}^{2}-1}\end{array}\right.$,即$\left\{\begin{array}{l}{0≤m≤2}\\{-\sqrt{2}≤m≤\sqrt{2}}\\{-2<m<1}\end{array}\right.$,
解得0≤m<1,
即m∈[0,1).
故答案为:[0,1).
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系是解决本题的关键.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
| 高效 | 非高效 | 统计 | |
| 新课堂模式 | 60 | 30 | 90 |
| 传统课堂模式 | 40 | 50 | 90 |
| 统计 | 100 | 80 | 180 |
| P(K2≧K0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
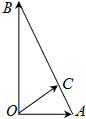
| A. | $\frac{1}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}$ | B. | $\frac{3}{4}\overrightarrow{OA}+\frac{1}{4}\overrightarrow{OB}$ | C. | $\frac{3}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ | D. | $\frac{5}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
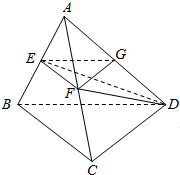 如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:
如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不必要也不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | $\frac{21}{3}$ | C. | $\frac{67}{6}$ | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com