
分析 由题意可得本题即求t=sin($\frac{x}{2}$-$\frac{π}{4}$)在函数值小于零时的增区间.再结合正弦函数的图象特征可得 2kπ-$\frac{π}{2}$≤$\frac{x}{2}$-$\frac{π}{4}$<2kπ,k∈Z,由此求得x的范围,即为所求.
解答 解:函数y=log${\;}_{\frac{1}{2}}$sin($\frac{π}{4}$-$\frac{x}{2}$)的单调递增区间,即函数y=sin($\frac{π}{4}$-$\frac{x}{2}$)在函数值大于零时的单调递减区间.
再根据y=sin($\frac{π}{4}$-$\frac{x}{2}$)=-sin($\frac{x}{2}$-$\frac{π}{4}$),可得本题即求t=sin($\frac{x}{2}$-$\frac{π}{4}$)在函数值小于零时的增区间.
再结合正弦函数的图象特征可得 2kπ-$\frac{π}{2}$≤$\frac{x}{2}$-$\frac{π}{4}$<2kπ,k∈Z,
求得4kπ-$\frac{π}{2}$≤x<4kπ+$\frac{π}{2}$,可得原函数的单调增区间为[4kπ-$\frac{π}{2}$,4kπ+$\frac{π}{2}$),k∈Z,
故答案为:[4kπ-$\frac{π}{2}$,4kπ+$\frac{π}{2}$),k∈Z.
点评 本题主要考查正弦函数的单调性,对数函数的定义域,体现了等价转化的数学思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 10×219 | C. | -10×218 | D. | -3×218 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
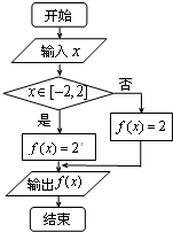 阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )
阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )| A. | (-∞,-2] | B. | (-∞,-2) | C. | [1,+∞) | D. | (-∞,-2)∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分(y≥0),A是曲线C1和C2的交点.已知∠AF2F1为钝角且|AF1|=$\frac{7}{2}$,|AF2|=$\frac{5}{2}$.
如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分(y≥0),A是曲线C1和C2的交点.已知∠AF2F1为钝角且|AF1|=$\frac{7}{2}$,|AF2|=$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 月份x | 1 | 2 | 3 | 4 |
| 用电量y | 45 | 40 | 30 | 25 |
| A. | 105 | B. | 51.5 | C. | 52 | D. | 52.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com