
分析 如图建立直角坐标系,设BF=k,k∈[0,3].得F(2-$\frac{1}{2}k$,$\frac{\sqrt{3}}{2}k$),E($\frac{3}{2}-\frac{1}{2}k$,$\frac{\sqrt{3}}{2}(k+1)$).
tan∠EAB=$\frac{\sqrt{3}(k+1)}{3-k}$,tan∠FAB=$\frac{\sqrt{3}k}{4-k}$,.tanθ=tan(∠EAB-∠FAB)=$\frac{\sqrt{3}}{{k}^{2}-k+3}$;即可求取值范围.
解答 解:如图建立直角坐标系,设BF=k,k∈[0,3].
∴∠B=60°,∴F(2-$\frac{1}{2}k$,$\frac{\sqrt{3}}{2}k$),E($\frac{3}{2}-\frac{1}{2}k$,$\frac{\sqrt{3}}{2}(k+1)$).
∴tan∠EAB=$\frac{\sqrt{3}(k+1)}{3-k}$,tan∠FAB=$\frac{\sqrt{3}k}{4-k}$,.
tanθ=tan(∠EAB-∠FAB)=$\frac{\sqrt{3}}{{k}^{2}-k+3}$;
∵k∈[0,3].∴${k}^{2}-k+3∈[\frac{11}{4},9]$,tanθ的取值范围是[$\frac{\sqrt{3}}{9},\frac{4\sqrt{3}}{11}$]
故答案为[$\frac{\sqrt{3}}{9},\frac{4\sqrt{3}}{11}$].
点评 本题考查了建立坐标系解决平面几何问题,属于难题.


科目:高中数学 来源: 题型:解答题
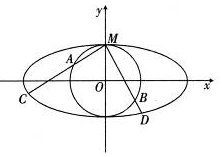 如图,圆O(O为坐标原点)与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于点M(0,1).
如图,圆O(O为坐标原点)与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于点M(0,1). 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}π}{8}$ | B. | $\frac{3\sqrt{3}π}{7}$ | C. | $\frac{3\sqrt{2}π}{8}$ | D. | $\frac{3\sqrt{2}π}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com