
分析 作出两曲线图象,根据交点个数判断直线的斜率范围即可.
解答 解:由y=1+$\sqrt{-{x}^{2}+2x}$得(x-1)2+(y-1)2=1(y≥1),
曲线C1表示以(1,1)为圆心以1为半径的上半圆,
显然直线y=1与曲线C1有两个交点,交点为半圆的两个端点.
∴直线y=kx+2k=k(x+2)与半圆有2个除端点外的交点,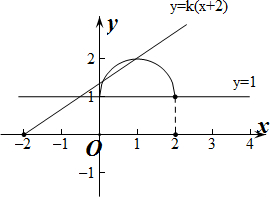
当直线y=k(x+2)经过点(0,1)时,k=$\frac{1}{2}$,
当直线y=k(x+2)与半圆相切时,$\frac{|3k-1|}{\sqrt{{k}^{2}+1}}$=1,解得k=$\frac{3}{4}$或k=0(舍),
∴当$\frac{1}{2}$<k<$\frac{3}{4}$时,直线y=k(x+2)与半圆有2个除端点外的交点,
故答案为:$(\frac{1}{2},\frac{3}{4})$
点评 本题考查了方程解与函数图象的关系,直线与圆的位置关系,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}或\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 没有使用联结词 | B. | 使用了逻辑联结词“或” | ||
| C. | 使用了逻辑联结词“且” | D. | 使用了逻辑联结词“非” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| A. | 0.25% | B. | 2.5% | C. | 97.5% | D. | 99.75% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,a} | B. | {1,2,3,a} | C. | {1,2,3} | D. | {1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com