
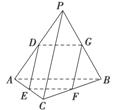
如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
(1)求证:DE∥平面BCP;
(2)求证:四边形DEFG为矩形;
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
解:
(1)证明:因为D,E分别为AP,AC的中点,所以DE∥PC.
又因为DE⊄平面BCP,
所以DE∥平 面BCP.
面BCP.
(2)证明:因为D,E,F,G分别为AP,AC,BC,PB的中点,
所以DE∥PC∥FG,DG∥AB∥EF,
所以四边形DEFG 为平行四边形.
为平行四边形.
又因为PC⊥AB,
所以DE⊥DG,
所以四边形DEFG为矩形.
(3)存在点Q满足条件,理由如下:
连接DF,EG,设Q为EG的中点.
由(2)知,DF∩EG=Q,且QD=QE=QF=QG=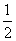 EG.
EG.
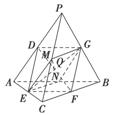
分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN.
与(2)同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,
且QM=QN=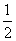 EG,
EG,
所以Q为满足条件的点.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
已知 甲命题:“如果直线a∥b,那么a∥α”;乙命题:“如果a∥平面α,那么a∥b”.要使上面两个命题成立,需分别添加的条件是( )
甲命题:“如果直线a∥b,那么a∥α”;乙命题:“如果a∥平面α,那么a∥b”.要使上面两个命题成立,需分别添加的条件是( )
A.甲:b⊂α;乙:b⊂α
B.甲:b⊂α;乙:a⊂β且α∩β=b
C.甲:a⊄α,b⊂α;乙:a⊂β且α∩β=b
D.甲:a⊄α,b⊂α;乙:b∥α
查看答案和解析>>
科目:高中数学 来源: 题型:
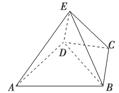
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
查看答案和解析>>
科目:高中数学 来源: 题型:
设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
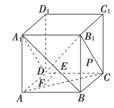
如图,在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1 及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是( )
及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是( )
A.线段B1C
B.线段BC1
C.BB1中点与CC1中点连成的线段
D.BC中点与B1C1中点连成的线段

查看答案和解析>>
科目:高中数学 来源: 题型:
如图,正方体ABCD-A1B1C1D1中,E是A1B上的点,F是AC上的点,且A1E=2EB,CF=2AF,则EF与平面A1B1CD的位置关系为____ ____.
____.
查看答案和解析>>
科目:高中数学 来源: 题型:
若某产品的直径长与标准值的差的绝对值不超过1 mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组 ,得到如下频率分布表:
,得到如下频率分布表:
| 分组 | 频数 | 频率 |
| [-3,-2) |
| 0.10 |
| [-2,-1) | 8 | |
| (1,2] |
| 0.50 |
| (2,3] | 10 | |
| (3,4] | ||
| 合计 | 50 | 1.00 |
(1)将上面表格中缺少的数据填在相应位置;
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品.据此估算这批产品中的合格品的件数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com