
分析 (Ⅰ)由题意a1=$\frac{1}{3}$,an=$\frac{{a}_{n-1}}{3{a}_{n-1}+1}$(代入计算,可求a2、a3、a4值,并根据规律猜想出数列{an}的通项公式;
(Ⅱ)检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答 解:(Ⅰ)a1=$\frac{1}{3}$,an=$\frac{{a}_{n-1}}{3{a}_{n-1}+1}$,
∴a2=$\frac{\frac{1}{3}}{3×\frac{1}{3}+1}$=$\frac{1}{6}$,a3=$\frac{\frac{1}{6}}{3×\frac{1}{6}+1}$=$\frac{1}{9}$,a4=$\frac{\frac{1}{9}}{3×\frac{1}{9}+1}$=$\frac{1}{12}$,
猜想:an=$\frac{1}{3n}$,
(Ⅱ):①当n=1时,猜想成立,
②假设n=k(k∈N*)时猜想成立,即ak=$\frac{1}{3k}$.
那么n=k+1时,ak+1=$\frac{{a}_{k}}{3{a}_{k}+1}$=$\frac{\frac{1}{3k}}{3•\frac{1}{3k}+1}$=$\frac{1}{3(k+1)}$
∴当n=k+1时猜想仍成立.
根据①②,可以断定猜想对任意的n∈N*都成立.
点评 本题主要考查归纳推理,数学归纳法.考查运算化简能力、推理论证能力、化归转化思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
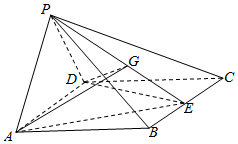 四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,∠APD=60°,E,G分别是BC,PE的中点
四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,∠APD=60°,E,G分别是BC,PE的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
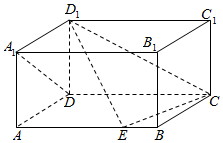 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com