
 如图,△ABC中,∠ACB=90°,D是AC上一点,以AD为直径作⊙O交AB于点G
如图,△ABC中,∠ACB=90°,D是AC上一点,以AD为直径作⊙O交AB于点G分析 (1)证明∠AGD=∠BCA=90°,可得B、C、D、G四点共圆
(2)利用切割线定理、射影定理,求出CP,即可求CD•CA的值.
解答 (1)证明:∵AD是直径,
∴∠AGD=90°,
∵∠BCA=90°,
∴∠AGD=∠BCA,
∴B、C、D、G四点共圆
(2)解:∵CP是⊙O的切线,CDA是⊙O的割线,
∴CP2=CD•CA,
∵∠CPO=90°,PH⊥AD,
∴CP2=CH•CO,
∵CH=$\frac{16}{5}$,OH=$\frac{9}{5}$,
∴CO=5,
∴CP2=CH•CO=16,
∴CD•CA=16.
点评 本题考查四点共圆、切割线定理、射影定理,考查学生的计算能力,比较基础.


科目:高中数学 来源: 题型:解答题
 如图,抛物线C1:y2=4x的焦准距(焦点到准线的距离)与椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长半轴相等,设椭圆的右顶点为A,C1,C2在第一象限的交点为B,O为坐标原点,且△OAB的面积为$\frac{{2\sqrt{6}}}{3}$
如图,抛物线C1:y2=4x的焦准距(焦点到准线的距离)与椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长半轴相等,设椭圆的右顶点为A,C1,C2在第一象限的交点为B,O为坐标原点,且△OAB的面积为$\frac{{2\sqrt{6}}}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,BC是圆O的一条弦,延长BC至点E,使得BC=2CE=2,过E作圆O的切线,A为切点,∠BAC的平分线AD交BC于点D,则DE的长为$\sqrt{3}$.
如图,BC是圆O的一条弦,延长BC至点E,使得BC=2CE=2,过E作圆O的切线,A为切点,∠BAC的平分线AD交BC于点D,则DE的长为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
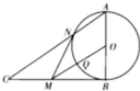 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作圆O与斜边AB交于N,过点O作OM∥AC,交BC于M,交圆O于Q.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径作圆O与斜边AB交于N,过点O作OM∥AC,交BC于M,交圆O于Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC的中点,点E1,F1分别是棱A1D1,C1D1的中点.求证:EE1∥FF1.
如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC的中点,点E1,F1分别是棱A1D1,C1D1的中点.求证:EE1∥FF1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com