
分析 (1)利用空间向量坐标运算法则能求出2$\overrightarrow{a}$+3$\overrightarrow{b}$,3$\overrightarrow{a}$-2$\overrightarrow{b}$,$\overrightarrow{a}$$•\overrightarrow{b}$的值,并能求出$\overrightarrow{a}$与$\overrightarrow{b}$所成角的余弦值.
(2)z轴的方向向量为(0,0,1),λ$\overrightarrow{a}$+μ$\overrightarrow{b}$=(3λ+2μ,5λ+μ,-4λ+8μ),由向量垂直的性质,能求出λ=2μ时,λ$\overrightarrow{a}$+μ$\overrightarrow{b}$与z轴垂直.
解答 解:(1)∵空间向量$\overrightarrow{a}$=(3,5,-4),$\overrightarrow{b}$=(2,1,8),
∴2$\overrightarrow{a}$+3$\overrightarrow{b}$=(6,10,-8)+(6,3,24)=(12,13,16),
3$\overrightarrow{a}$-2$\overrightarrow{b}$=(9,15,-12)-(4,2,16)=(5,13,-28),
$\overrightarrow{a}$$•\overrightarrow{b}$=6+5-32=-21,
∴$\overrightarrow{a}$与$\overrightarrow{b}$所成角的余弦值为:cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{-21}{\sqrt{9+25+16}•\sqrt{4+1+64}}$=-$\frac{7\sqrt{138}}{230}$.
(2)z轴的方向向量为(0,0,1),
λ$\overrightarrow{a}$+μ$\overrightarrow{b}$=(3λ+2μ,5λ+μ,-4λ+8μ),
∵λ$\overrightarrow{a}$+μ$\overrightarrow{b}$与z轴垂直,则0•(3λ+2μ)+0•(5λ+μ)+(-4λ+8μ)=0,即8μ-4λ=0,∴λ=2μ.
∴λ=2μ时,λ$\overrightarrow{a}$+μ$\overrightarrow{b}$与z轴垂直.
点评 本题考查平面向量的坐标运算,考查向量所成角的余弦值的求法,考查向量垂直的条件的判断与应用,是基础题,解题时要认真审题,注意向量坐标运算法则的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
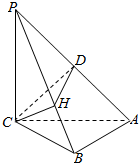 在三棱锥P-ABC中,PC⊥平面ABC,△PAC是等腰直角三角形,PA=6,AB⊥BC,CH⊥PB,垂足为H,D为PA的中点,则当△CDH的面积最大时,CB=$\sqrt{6}$.
在三棱锥P-ABC中,PC⊥平面ABC,△PAC是等腰直角三角形,PA=6,AB⊥BC,CH⊥PB,垂足为H,D为PA的中点,则当△CDH的面积最大时,CB=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com