
(本小题满分14分) 求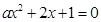 至少有一个负实根的充要条件。
至少有一个负实根的充要条件。
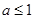 。
。
解析试题分析:(1)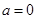 时为一元一次方程,其根为
时为一元一次方程,其根为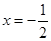 ,符合题目要求;…..3分
,符合题目要求;…..3分
(2)当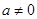 时,为一元二次方程,它有实根的充要条件是判断式
时,为一元二次方程,它有实根的充要条件是判断式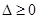 ,即
,即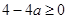 ,从而
,从而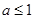 。………….6分
。………….6分
①又设方程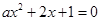 的两根为
的两根为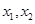 ,则由韦达定理得
,则由韦达定理得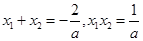 。因而方程
。因而方程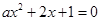 有一个负实根的充要条件是
有一个负实根的充要条件是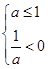 ,得
,得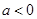 。……..9分
。……..9分
①②方程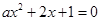 有两个负根的充要条件是
有两个负根的充要条件是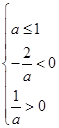 ,即
,即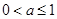 。….12分
。….12分
综上,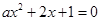 至少有一个负实根的充要条件是:
至少有一个负实根的充要条件是: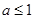 ………..14分
………..14分
考点:一元二次方程的根的分布与系数的关系;必要条件、充分条件与充要条件的判断
点评:⑴本题主要考查一个一元二次方程根的分布问题.在二次项系数不确定的情况下,一定要分二次项系数分为0和不为0两种情况讨论.
⑵设一元二次方程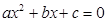 (
(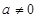 )的两个实根为
)的两个实根为 ,
,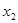 ,且
,且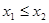 。
。
① 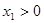 ,
,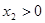 (两个正根)
(两个正根)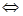
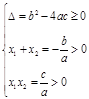 ;
;
② 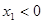 ,
,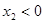 (两个负根)
(两个负根)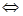
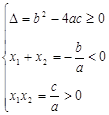 ;
;
③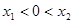 (一个正根一个负根)
(一个正根一个负根)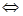
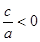 。
。


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
已知函数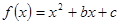 ,且
,且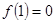
(1)若函数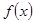 是偶函数,求
是偶函数,求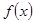 的解析式;(3分)
的解析式;(3分)
(2)在(1)的条件下,求函数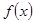 在
在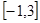 上的最大、最小值;(3分)
上的最大、最小值;(3分)
(3)要使函数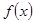 在
在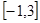 上是单调函数,求
上是单调函数,求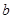 的范围。(4分)
的范围。(4分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)已知函数
(1)当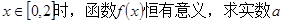 的取值范围;
的取值范围;
(2)是否存在这样的实数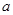 ,使得函数
,使得函数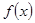 在区间
在区间 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出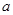 值;若不存在,说明理由。
值;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为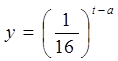 (a为常数),
(a为常数),
如图所示,根据图中提供的信息,回答下列问题: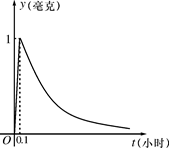
(Ⅰ)从药物释放开始,求每立方米空气中的含药量
y(毫克)与时间t(小时)之间的函数关系式?
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过多少小时后,学生才能回到教室.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com