
(本题满分10分)已知函数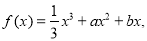 且
且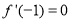
(1)试用含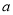 的代数式表示
的代数式表示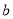 ;
;
(2)求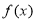 的单调区间;
的单调区间;
(3)令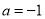 ,设函数
,设函数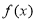 在
在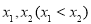 处取得极值,记点
处取得极值,记点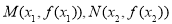 ,证明:线段
,证明:线段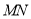 与曲线
与曲线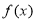 存在异于
存在异于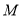 、
、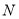 的公共点;
的公共点;
(1)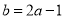 ;(2)当
;(2)当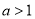 时,函数
时,函数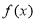 的单调增区间为
的单调增区间为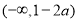 和
和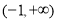 ,单调减区间为
,单调减区间为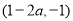 ;当
;当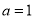 时,函数
时,函数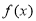 的单调增区间为R;当
的单调增区间为R;当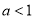 时,函数
时,函数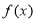 的单调增区间为
的单调增区间为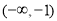 和
和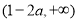 ,单调减区间为
,单调减区间为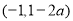 ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)求导,利用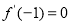 进行求解;(2)求导,利用分类讨论思想讨论两根的大小关系研究其单调区间;(3)构造函数
进行求解;(2)求导,利用分类讨论思想讨论两根的大小关系研究其单调区间;(3)构造函数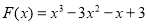 ,证明
,证明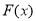 在区间
在区间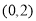 上有零点.
上有零点.
解题思路:1.研究函数的单调性,往往利用其导函数进行证明;2.证明直线与曲线的公共点的个数问题,往往可转化为函数的零点的个数问题.
试题解析:(1)依题意,得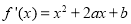
由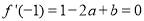 得
得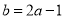
(2)由(1)得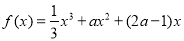
故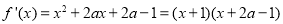
令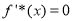 ,则
,则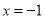 或
或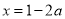
①当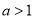 时,
时,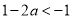
当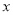 变化时,
变化时,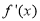 与
与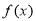 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| + | — | + |
| 单调递增 | 单调递减 | 单调递增 |
由此得,函数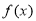 的单调增区间为
的单调增区间为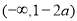 和
和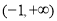 ,单调减区间为
,单调减区间为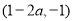
②由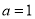 时,
时,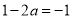 ,此时,
,此时,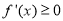 恒成立,且仅在
恒成立,且仅在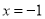 处
处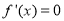 ,故函数
,故函数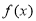 的单调区间为R
的单调区间为R
③当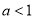 时,
时,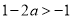 ,同理可得函数
,同理可得函数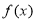 的单调增区间为
的单调增区间为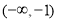 和
和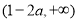 ,单调减区间为
,单调减区间为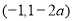
综上:
当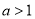 时,函数
时,函数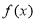 的单调增区间为
的单调增区间为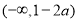 和
和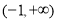 ,单调减区间为
,单调减区间为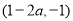 ;
;
当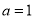 时,函数
时,函数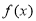 的单调增区间为R;
的单调增区间为R;
当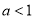 时,函数
时,函数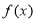 的单调增区间为
的单调增区间为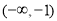 和
和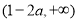 ,单调减区间为
,单调减区间为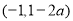
(3)当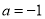 时,得
时,得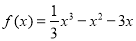
由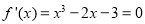 ,得
,得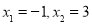
由(2)得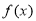 的单调增区间为
的单调增区间为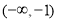 和
和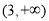 ,单调减区间为
,单调减区间为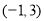
所以函数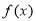 在
在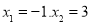 处取得极值。
处取得极值。
故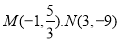
所以直线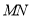 的方程为
的方程为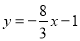
由 得
得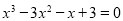
令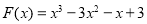
易得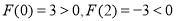 ,而
,而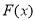 的图像在
的图像在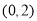 内是一条连续不断的曲线,
内是一条连续不断的曲线,
故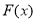 在
在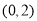 内存在零点
内存在零点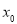 ,这表明线段
,这表明线段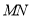 与曲线
与曲线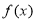 有异于
有异于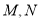 的公共点
的公共点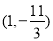 .
.
考点:1.函数的单调性;2.函数的零点个数问题;3.导数的应用.
考点分析: 考点1:导数及其应用 试题属性

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源:2014-2015学年吉林省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
如图,已知椭圆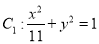 ,双曲线
,双曲线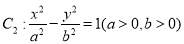 ,若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )
,若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )
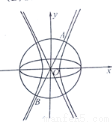
A.5 B.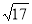 C.
C.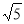 D.
D.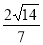
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
设数列{an}的前n项和为Sn,点 (n∈N*)均在函数
(n∈N*)均在函数 的图象上,则a2014=( )
的图象上,则a2014=( )
A.2014 B.2013 C.1012 D.1011
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省株洲市高二上学期期末文科数学试卷(解析版) 题型:解答题
(本题满分6分)某校高二年级的一次数学考试中,为了分析学生的得分情况,随机抽取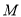 名同学的成绩,数据的分组统计表如下:
名同学的成绩,数据的分组统计表如下:
分组 | 频数 | 频率 | 频率/组距 |
(40,50] | 2 | 0.02 | 0.002 |
(50,60] | 4 | 0.04 | 0.004 |
(60,70] | 11 | 0.11 | 0.011 |
(70,80] | 38 | 0.38 | 0.038 |
(80,90] |
|
|
|
(90,100] | 11 | 0.11 | 0.011 |
合计 |
|
|
|
(1)求出表中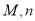 的值;
的值;
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在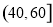 中的6位同学中任意抽取2人进行调查,求分数在
中的6位同学中任意抽取2人进行调查,求分数在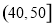 和
和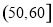 中各有一人的概率.
中各有一人的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省株洲市高二上学期期末文科数学试卷(解析版) 题型:选择题
有下列命题是假命题的是: ( )
A.双曲线 与椭圆
与椭圆 有相同的焦点;
有相同的焦点;
B. 是“x2-2x-3<0” 充分不必要条件;
是“x2-2x-3<0” 充分不必要条件;
C.“若xy=0,则x、y中至少有一个为0”的否命题是真命题.;
D. ”
”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com