
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 由题意可得曲线和直线均过原点,判断f(x)为奇函数且在R上递增,当直线y=kx与曲线相切,切点为(0,0),求得切线的斜率为2,讨论k的变化,即可得到符合题意的k的最大值.
解答 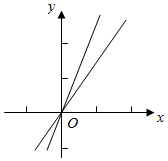 解:由曲线f(x)=ex-$\frac{1}{e^x}$与直线y=kx均过原点(0,0),
解:由曲线f(x)=ex-$\frac{1}{e^x}$与直线y=kx均过原点(0,0),
由f(-x)=e-x-ex=-(ex-e-x)=-f(x),
可得f(x)为奇函数,图象关于原点对称,
且f′(x)=ex+e-x>0,f(x)在R上递增,
由题意可得f(x)与直线y=kx有且仅有交点为(0,0),
当直线y=kx与曲线相切,切点为(0,0),
切线的斜率为k=e0+e0=2,
当k<0时,显然只有一个交点(0,0),
当0≤k≤2时,显然只有一个交点(0,0),
当k>2时,有3个交点.
则符合条件的k的最大值为2.
故选:D.
点评 本题考查导数的运用:求切线的斜率,考查函数方程的转化思想以及数形结合的思想方法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (x+1)2+(y-2)2=5 | B. | (x-2)2+(y-1)2=5 | C. | (x-1)2+(y+2)2=5 | D. | (x-2)2+(y+1)2=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{{\sqrt{2}}}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
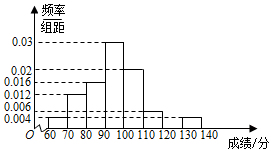 某校在一次期末考试中,全校学生的数学成绩都介于60分到140分之间(满分150分),为了估计该校学生的数学考试情况,从该校2000名学生的数学成绩中随机抽取50名学生的数学成绩,将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140].如图是按照上述分组得到的频率分布直方图的一部分.估计该校2000名学生这次考试的数学成绩的平均分为97.
某校在一次期末考试中,全校学生的数学成绩都介于60分到140分之间(满分150分),为了估计该校学生的数学考试情况,从该校2000名学生的数学成绩中随机抽取50名学生的数学成绩,将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140].如图是按照上述分组得到的频率分布直方图的一部分.估计该校2000名学生这次考试的数学成绩的平均分为97.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
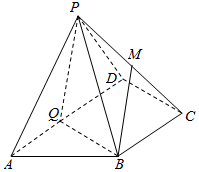 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=90°,AD∥BC,平面PAD⊥底面ABCD,BC=$\frac{1}{2}$AD,PA=PD=AB=2,M,Q为AD,PC的中点
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=90°,AD∥BC,平面PAD⊥底面ABCD,BC=$\frac{1}{2}$AD,PA=PD=AB=2,M,Q为AD,PC的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com