
分析 根据等比数列的前n项和公式得到Tn,分离参数,设cn=$\frac{2n-4}{{3}^{n}}$,利用作差确定数列{cn}的单调性,求出数列的最大值即可
解答 解:当n=1时,Tn=$\frac{9}{2}$,
当n≥2时,Tn=a1+a2+…+an=$\frac{9}{2}$+$\frac{9(1-{3}^{n-1})}{1-3}$=$\frac{1}{2}$×3n+1,
∵对任意的n∈N*都有Tn•k≥3n-6恒成立,
∴$\frac{1}{2}$×3n+1•k≥3n-6,
∴k≥$\frac{2n-4}{{3}^{n}}$,
设cn=$\frac{2n-4}{{3}^{n}}$,
则cn+1-cn=$\frac{2(n+1)-4}{{3}^{n+1}}$-$\frac{2n-4}{{3}^{n}}$=$\frac{2(5-2n)}{{3}^{n+1}}$
当n≤2时,cn+1>cn,当n≥3时,cn+1<cn,
∴cn的最大项是c3=$\frac{2}{27}$,
∴k≥$\frac{2}{27}$,
故答案为:k≥$\frac{2}{27}$
点评 本题考查了an与Tn的关系,以及等比数列的前n项和公式,数列的恒成立转化为求数列的最大项问题,通过作差研究数列的单调性也是常用的方法,难度较大,一定要注意n的取值范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{π}$ | B. | $\frac{1}{π}$ | C. | $-\frac{1}{π^2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\vec a$-$\vec b$ | B. | $\vec b$-$\vec a$ | C. | $\frac{1}{2}$($\vec a$-$\vec b$) | D. | $\frac{1}{2}$($\vec b$-$\vec a$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
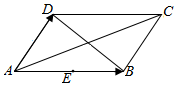
| A. | $\overrightarrow{AC}$=$\overrightarrow a$+$\overrightarrow b$ | B. | $\overrightarrow{BD}$=$\overrightarrow a$-$\overrightarrow b$ | C. | $\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow a$ | D. | $\overrightarrow{CB}$=-$\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com