
分析 根据角的定义和三角函数符号判断.
解答 解:①∵α<β,∴α-β<0,故①错误;
②若α是第一象限角,则2kπ<α<$\frac{π}{2}+2kπ$,
∴kπ$<\frac{α}{2}<\frac{π}{4}+kπ$,∴$\frac{α}{2}$在第一、三象限.故②正确.
③∵sin2θ+cos2θ=1,∴($\frac{m-3}{m+5}$)2+($\frac{4-2m}{m+5}$)2=1,
解得m=0或m=8.故③错误.
④∵sin$\frac{θ}{2}$=$\frac{3}{5}$,cos$\frac{θ}{2}$=-$\frac{4}{5}$,∴$\frac{θ}{2}$=143°+360°•k
∴θ=286°+360°•2k.
∴θ在第四象限.故④正确.
故答案为:②④.
点评 本题考查了角的定义,象限角的三角函数的符号,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
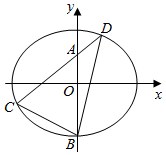 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
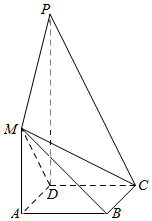 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com